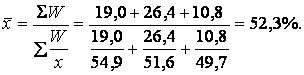6.4. Інші види середніх величин. Методика визначення середнього значення відносної величини.
Обмежене використання у статистиці знаходять середня квадратична та середня геометрична величини. Середня квадратична (проста і зважена) обчислюються за формулами:
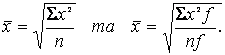
Вона використовується при розрахунках показників варіації (середнього квадратичного відхилення) у модифікованому вигляді.
Середня геометрична величина застосовується тоді, коли обсяг ознаки дорівнює не сумі, а добутку варіант. Її формула має вигляд:
![]()
За наведеною формулою підраховується середній коефіцієнт росту, при цьому Х – ланцюгові коефіцієнти росту.
У окремих випадках виникає потреба визначити узагальнений середній показник по декількох ознаках одночасно. Він має назву багатомірної середньої. При цьому осереднюються не абсолютні значення ознак, а коефіцієнти відношення до середнього рівня по кожній ознаці. Названі коефіцієнти визначаються за формулою:
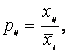
де і = 1, 2, 3, ....... , m — число ознак;
j = 1, 2, 3, ....... , n — число одиниць у сукупності.
Багатомірна середня має вигляд:
 .
.
Приклад розрахунку багатомірної середньої:
|
Одиниці сукупності (j) | Ознаки (і) |
p1j |
p2j |
p3j |
| ||
| х1 | х2 | х3 | |||||
| 1 | 17 | 110 | 2720 | 0,850 | 1,222 | 1,001 | 1,024 |
| 2 | 21 | 80 | 3516 | 1,050 | 0,889 | 1,294 | 1,078 |
| 3 | 18 | 95 | 1790 | 0,900 | 1,056 | 0,659 | 0,872 |
| 4 | 25 | 75 | 2844 | 1,250 | 0,833 | 1,010 | 1,031 |
| В середньому | 20 | 90 | 2718 | 1,000 | 1,000 | 1,000 | х |
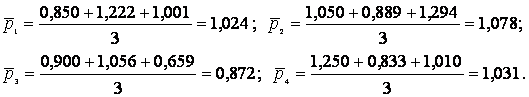
Отже, найвищий рівень за трьома ознаками одночасно має друга одиниця сукупності (![]() = 1,078), найнижчий — третя (
= 1,078), найнижчий — третя (![]() = 0,872).
= 0,872).
У статистичному аналізі досить часто необхідно визначити середнє значення не абсолютної, а відносної величини. Методика розрахунку середньої в даному випадку залежить від вихідних даних. Якщо відомі значення показників, що знаходяться у чисельнику та знаменнику відносної величини, використовується формула:
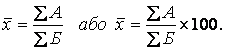
У тому випадку, коли відомі значення осереднюваної відносної величини (ВВ), які розглядаються як варіанти Х, та значення показника, що знаходиться у її знаменнику (Б) і виконує роль частоти f, розрахунок виконується за формулою середньої арифметичної зваженої:
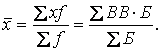
Наприклад, відома питома вага міського населення (ВВ) та загальна чисельність всього населення (Б) по трьох районах області:
ВВ (х) Б (f)
1-й район: 45,1% та 34,6 тис. чол.
2-й район: 48,4% та 51,2 тис. чол.
3-й район: 50,3% та 21,7 тис. чол.
Середня питома вага міського населення становить:
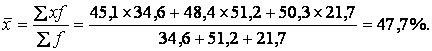
В тому випадку, коли відомі значення осереднюваного показника (ВВ) та значення, що знаходяться в його чисельнику (А) і виконують роль обсягу ознаки (W), розрахунок середньої здійснюється за формулою гармонійної зваженої:
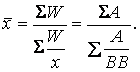
Наприклад, відома питома вага жінок та їх чисельність по трьох районах області:
ВВ (х) А (W)
1-й район: 54,9% та 19,0 тис. чол.
2-й район: 51,6% та 26,4 тис. чол.
3-й район: 49,7% та 10,8 тис. чол.
Середня питома вага жінок становить: