6.7. Аналіз дохідності операцій із цінними паперами
6.7. Аналіз дохідності операцій із цінними паперами
Для порівняння та оцінки акцій, що обертаються на ринку і є об’єктом інвестицій, використовують ряд показників, суть яких наведено нижче.
Дохід у розрахунку на одну просту акцію позначають усталеним показником EPS (earning per share), який визначається як чистий прибуток на одну акцію (у разі, якщо в статутному фонді емітента є привілейовані акції, слід зменшити суму прибутку, яка розподіляється, на суму виплат за привілейованими акціями).
Поєднання суб’єктивних очікувань багатьох інвесторів формує ринковий попит на акції, унаслідок чого можна визначити співвідношення між їх ринковою ціною та річним доходом на акцію (price to earning ratio, P/E), яке є визначальним для пошуку недооцінених акцій і визначається співвідношенням ринкової ціни акції до її показника EPS.
Крім цих двох показників, для власників суттєвим є показник дивідендного покриття (dividend cover, DC), яке визначається співвідношенням EPS до суми дивіденду на одну просту акцію.
Для оцінки ефективності фінансових інвестицій використовують поняття дохідності інвестицій (simple rate of return, SRR; probability of investments), який є досить простим і тому використовується часто для оцінки діяльності:
![]() ,
,
де NP — чистий прибуток за певний інтервал часу;
TIC — інвестиційні витрати (вкладення) за цей інтервал часу.
Порівнюючи цей показник із планованим рівнем дохідності, інвестор має можливість зробити висновок, чи справдились його очікування щодо інвестування.
Недоліком цього показника є те, що він не враховує вартості грошей у часі, а також час виникнення грошових потоків та їх
узгодженість.
Серед боргових зобов’язань, що перебувають в обігу, найбільш значну групу складають ЦП, що дають фіксований прибуток (fixed income securities). Прикладами подібних ЦП є облігації, депозитні сертифікати та деякі інші види зобов’язань. До цього виду цінних паперів можна також віднести і привілейовані акції (preferred stocks), якщо за ними регулярно виплачується фіксований дивіденд.
Як правило, будь-який борговий ЦП має такі основні характеристики: номінальна вартість (par value, face value), купонна ставка прибутковості (coupon rate), дата випуску (date of issue), дата погашення (date of maturity), сума погашення (redemption value). Найважливішу роль в аналізі цінних паперів відіграють дата і ціна їх придбання, а також середня тривалість платежів (duration).
Номінальна вартість — це сума, вказана на бланку ЦП, або в умовах випуску. Під час погашення боргового ЦП власникові повертається його номінальна вартість та, як правило, сплачується процентний дохід. Однак поточна ціна ЦП може не збігатися з номіналом і залежить від ситуації на ринку. Якщо ціна, сплачена за ЦП, нижча за номінал, говорять, що облігація продана зі знижкою або з дисконтом (discount bond), а якщо вище — з премією (premium bond).
Купонна норма прибутковості — це процентна ставка, за якою власникові облігації виплачується періодичний прибуток. Відповідно сума періодичного прибутку дорівнює добутку купонної ставки на номінальну вартість облігації і виплачується кожного купонного періоду (раз у рік, півріччя або квартал).
Дата погашення — дата викупу облігації емітентом у її власника (як правило, за номіналом). Дата погашення вказується в умовах випуску облігації. На практиці в аналізі важливу роль відіграє загальний термін обігу (maturity period) облігації, а також дата її купівлі (settlement date).
Для короткострокових боргових ЦП їх розміщення часто здійснюється за ціною, що менше їх номінальної вартості, а погашення — за номінальною вартістю. У цьому разі ЦП на ринку буде продаватися з дисконтом. Норма прибутковості, яку отримає інвестор, залежить від різниці між ціною купівлі — Р і номінальною вартістю N (ціною погашення). Оскільки номінал облігації відомий (або може бути взятий за 100 %), для визначення прибутковості операції досить знати дві величини — ціну купівлі P (або курс K) на дату проведення операції і термін до погашення в днях — t.
Розрахунок ціни придбання P дисконтних облігацій здійснюється з урахуванням простих процентів за річною ставкою Y (у будь-який момент до дати погашення, на первинному або вторинному ринку):
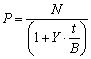 ,
,
де t — число днів до погашення;
Y — річна ставка процентів;
N — номінал;
В — часова база (360 для звичайних; 365 або 366 для точних процентів).
Приклад 9. Яку ціну готовий заплатити інвестор за дисконтну облігацію з номіналом у 1000,00 грн і погашенням через 90 днів, якщо бажана норма прибутковості 12 % річних?
P = 1000 / (1 + 0,12 · 90/365) = 971,2 грн.
Отже, процес оцінки вартості дисконтної облігації полягає у визначенні сучасної величини елементарного потоку платежів за формулою простих процентів виходячи з необхідної норми прибутковості (ринкової ставки) Y.
Тоді курсова вартість (курс) дисконтної облігації в будь-який момент часу обчислюється за формулою:
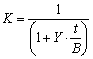 ,
,
де t — число днів до погашення на дату оцінки;
Y — річна ставка процентів;
В — часова база (тривалість календарного року — 360 або 365/366 днів).
Ціна процентного боргового зобов’язання з виплатою процентів у момент погашення дорівнює поточній вартості майбутніх потоків платежів, розрахованій за простими процентами, яка забезпечує отримання необхідної норми прибутковості (прибутковість до погашення). З урахуванням накопиченого на момент проведення операції доходу S, вартість Р1, що відповідає необхідній нормі прибутковості Y, може бути визначена з такого співвідношення:
де t — число днів до погашення.
При Y = r ринкова вартість зобов’язання на момент випуску буде рівна номіналу (тобто Р1 = N). При Y > r, відповідно P1 < N, і борговий ЦП буде розміщуватися з дисконтом, а у випадку Y < r — з премією (тобто P1 > N). Оскільки випуск облігацій передбачає реєстрацію умов їх випуску із заздалегідь оголошеною дохідністю, на практиці часто трапляються випадки, коли у зв’язку зі змінами на дату реалізації облігацій норми прибутковості, якої вимагають інвестори, процентні облігації навіть у випадку первинного розміщення розміщуються не за номінальною вартістю, а з дисконтом (якщо вимагається вища дохідність від оголошеної) або з премією (якщо інвестори задовольняються дохідністю, нижчою від оголошеної).
На дату, що не збігається з датою початку розміщення, ринкова вартість боргового ЦП з урахуванням накопиченого доходу може відхилятися від номінальної вартості. Подібні відхилення на дату операції заведено котирувати у процентах до номінальної вартості ЦП. При цьому оголошена ставка доходу за зобов’язанням r показується окремо. Курсова вартість K боргового зобов’язання визначається при цьому як:
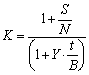 ,
,
де t — кількість днів до погашення;
N — номінальна вартість;
S — абсолютна величина доходу, накопичена до дати здійснення операції.
Оскільки величина S може бути знайдена зі співвідношення:
![]() ,
,
де t1 — кількість днів від моменту випуску до дати операції, повна ринкова вартість Р1 боргового ЦП може бути також визначена як сума номінальної вартості ЦП N та накопиченого процентного доходу S:
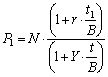 .
.
Розрахунок дохідності короткострокових облігацій, які розміщуються з дисконтом, здійснюється за формулою простих процентів. У цьому випадку формула для визначення прибутковості короткострокового зобов’язання може мати такий вигляд:
![]() ,
,
де t — число днів до погашення;
Р1 — ціна купівлі;
N — номінал;
К — курсова вартість;
В — часова база (360 — для звичайних; 365 або 366 — для точних процентів).
Приклад 10. Короткострокові державні облігації з терміном погашення 90 днів було придбано за ціною 98,22 % від номінальної вартості. Визначити прибутковість операції для інвестора:
а) з використанням звичайних процентів;
б) з використанням точних процентів.
а) Y = (100 – 98,22) / 98,22 · 360 / 90 = 0,0725, або 7,25 % річних;
б) Y = (100 – 98,22) / 98,22 · 365 / 90 = 0,07349, або 7,35 % річних.
Зауважимо, що розраховані за формулою простих процентів показники мають, як мінімум, два недоліки:
їх не можна використати для порівняння ефективності проведення короткострокових операцій з іншими видами інвестицій, у тому числі — довгостроковими;
вони не враховують можливості неодноразового реінвестування отриманих прибутків протягом року за деякими видами короткострокових зобов’язань (наприклад депозитних сертифікатів НБУ, три- або шестимісячних ОВДП тощо).
Для подолання вказаних обмежень використовують більш універсальний показник — ефективна прибутковість (припущення про багаторазове реінвестування більш коректно враховує формула прирощення за складними процентами).
У зв’язку з цим для розрахунку прибутковості короткострокового зобов’язання може бути використана така формула ефективної прибутковості (yield to maturity, YTM):
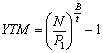 ,
,
де t — число днів до погашення;
Р1 — ціна купівлі;
N — номінал;
В — часова база (360 — для звичайних; 365 або 366 — для точних процентів).
Для прикладу 10 розрахунок прибутковості YTM для короткострокового зобов’язання за точними процентами дає результат:
YTM = (100 / 98,22)365 / 90 – 1 = 0,075, або 7,5 % річних.
Розрахункові дані щодо прибутковості за різними методами обчислення зведемо для порівняння в табл. 6.10.
Таблиця 6.10
ПОРІВНЯННЯ ПРИБУТКОВОСТІ ІНВЕСТИЦІЙ У ЦП
ЗА ПРОСТИМИ (звичайними та точними) І СКЛАДНИМИ ПРОЦЕНТАМИ
| Прості проценти | Кількість днів | Термін | Ціна | Дохід при погашенні, грн | Прибутковість для інвестора, % |
| Звичайні проценти | 360 | 90 | 98,22 | 1,78 | 7,25 |
| Точні проценти | 365 | 90 | 98,22 | 1,78 | 7,35 |
| Складні проценти | 365 | 90 | 98,22 | 1,78 | 7,50 |
Як висновок, зауважимо, що хоча дисконтування за формулою складних процентів проводиться, як правило, лише для довгострокових інвестицій, показник YTM, котрий визначається за формулою складних процентів, може бути використаний для порівняння ефективності операцій, що проводяться з цінними паперами, які мають різні терміни погашення (в тому числі і короткострокових). Але оскільки для різних боргових ЦП періодичність нарахування процентів (сплати доходу) може суттєво відрізнятися, показники YTM будуть незіставними. У цьому разі доцільно використовувати ефективну річну ставку ref :
![]() ,
,
де rn — номінальна річна процентна ставка;
k — кількість нарахувань процентних доходів за рік.
Якщо короткострокова безкупонна облігація купується з метою подальшої реалізації (тобто для проведення арбітражних операцій), її прибутковість визначається цінами і термінами купівлі-продажу:
![]() ;
;
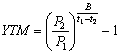 .
.
У цьому випадку в момент за t2 днів до погашення ціна перепродажу P2, що забезпечує отримання необхідної норми прибутковості Y, визначається з такого співвідношення:
![]() ,
,
t1 — число днів до погашення в момент купівлі;
t2 — число днів до погашення в момент перепродажу.
Розглянемо питання визначення дохідності за процентними борговими цінними паперами, які розміщуються за номінальною вартістю, а проценти виплачуються в момент погашення. До цього виду цінних паперів, відносять, як правило, депозитні (ощадні сертифікати) банків, короткострокові облігації, а також векселі з нарахуванням процентів. Для простоти далі розглянемо прибутковість тільки для депозитних сертифікатів.
Дохід за сертифікатом виплачується в момент погашення разом з основною сумою боргу, виходячи з обумовленої при розміщенні сертифіката процентної ставки r.
З урахуванням введених раніше позначень, абсолютний розмір доходу за сертифікатом S може бути визначений так:
![]() ,
,
r — процентна ставка за сертифікатом;
t — термін до дати погашення в днях;
В — часова база (360 — для звичайних; 365 або 366 — для точних відсотків).
Відповідно річна прибутковість до погашення Y, обчислена за формулою простих відсотків, буде дорівнювати:
![]()
З цього випливає, що коли зобов’язання розміщене за номіналом і пред’явлене до погашення у визначений термін, його прибутковість буде рівна оголошеній ставці процентів (тобто Y = r).
Якщо сертифікат продається (купується) між датами випуску і погашення, абсолютна величина прибутку S буде розподілена між покупцем і продавцем відповідно до ринкової ставки (норми прибутковості покупця) Y за аналогічними ЦП на даний момент часу і пропорційна терміну володіння ЦП кожною зі сторін. Частина прибутку, належна покупцеві (S2) за термін t2, що залишився до дати погашення, дорівнюватиме:
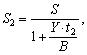
де t2 — число днів від моменту купівлі до дати погашення сертифіката.
Відповідно продавець отримає величину доходу S1:
Зазначені співвідношення відображають ситуацію рівноваги на ринку (тобто «справедливого» розподілу доходів відповідно до ринкової ставки Y і пропорційно терміну володіння ЦП кожною зі сторін). Будь-яке відхилення в той чи інший бік спричинить перерозподіл доходу на користь одного з учасників операції. Неважко помітити, що при r < Y накопичений прибуток продавця буде нижчим за обіцяний за умовами випуску.
Гранична величина ринкової ставки Y, за якої продавець ЦП все ще отримує прибуток, повинна задовольняти нерівності:
де r — ставка за сертифікатом;
Y — ринкова ставка;
t1 — число днів до погашення в момент купівлі;
t2 — число днів до погашення в момент перепродажу.
При цьому прибутковість операції для продавця буде дорівнювати:
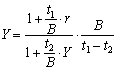 ;
;
Приклад 11. Пакет дисконтних облігацій сумарним номіналом 500 000,00 грн, ціна яких на вторинному ринку визначається поточними процентними ставками, куплено за 6 місяців до погашення, а продано за 3 місяці до погашення. Процентні ставки складали 40 і 30 % відповідно. За якою ціною здійснювались операції купівлі-продажу цього пакета облігацій? Який дохід та дохідність цієї операції?
Ціна купівлі складала 500 000,00 · (1 – 0,50 · 0,4) = 400 000,00 грн.
Ціна продажу 500 000,00 · (1 – 0,25 · 0,3) = 462 500,00 грн, тобто дохід за 1/4 року склав 62 500,00 грн, дохідність зазначеної операції становить: 62 500,00 / 400 000,00 / (1/4) · 100 % = 62,5 % річних.
Якби процентні ставки не падали, а, навпаки, зростали (наприклад, з 30 до 40 % за цей же період), то:
ціна купівлі складала б 500 000,00 · (1 – 0,50 · 0,3) = 425 000,00 грн;
ціна продажу 500 000,00 · (1 – 0,25 · 0,4) = 450 000,00 грн,
тобто дохід за 1/4 року склав 25 000,00 грн, дохідність зазначеної операції становить: 25 000,00 / 425 000,00 / (1/4) · 100 % = 23 % річних.
Отже, при падінні процентних ставок інвестор отримує вищу дохідність (62,5 проти 40 %, якби ЦП утримував до погашення), а при зростанні процентних ставок інвестор отримує меншу дохідність (в нашому прикладі — 23 проти 30 %, якби ЦП утримувались до погашення).
Під час періодичних купонних виплат за борговими ЦП доводиться оцінювати у часі не одиничні грошові суми, а потоки грошових коштів. Обчислення дисконтованої оцінки сум грошових коштів у цьому випадку здійснюється через використання відповідних формул для кожного елемента грошового потоку. Елемент грошового потоку заведено позначати CFk (від cash flow), де k — номер періоду, в який розглядається грошовий потік. Грошовий потік, який складається з однакових грошових сум, називається ануїтетом.
У випадку n рівних за обсягом купонних виплат формула для суми процентних виплат PV % за купонною облігацією, що має n купонів, буде мати вигляд:
![]() ,
,
а сумарний грошовий потік інвестору, включаючи погашення, становитиме:
де PVn — поточна вартість номінала N цінного папера;
PV % — поточна вартість усіх процентних виплат;
CFk — абсолютна вартість k-ї процентної виплати.
Аналогічна формула використовується для оцінки поточної вартості нескінченного (за часом) потоку грошових коштів (наприклад, за привілейованими акціями), яка обчислюється підсумовуванням нескінченного ряду (припускаючи, що CFk = CF = const):
У разі короткотермінового володіння цінними паперами, за якими, наприклад, дохід від зазначеного володіння складається із можливих дивідендних або процентних виплат D і зміни курсової вартості ЦП, дохідність становить:
![]() ,
,
де Sin — ціна купівлі ЦП;
Sout — ціна продажу ЦП;
t — кількість днів володіння ЦП;
В — часова база (360 — для звичайних; 365 або 366 — для точних процентів).

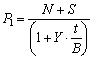 ,
,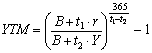 .
.