7.1. Виробничі функції

7.1. Виробничі функції

Поняття виробничої функції (ВФ) виникло з огляду на потребу відбити залежність між обсягом продукції, що виробляється, і ком­понентами витрат ресурсів (праці та капіталу). Американський еко­номіст П. Дуглас помітив, що співвідношення доходів від праці та капіталу в національному доході США майже не змінюється з часом. Цей висновок підтвердили подальші емпіричні дослідження для різних країн світу.

Описуючи виробничу підсистему економіки за допомогою ВФ, цю підсистему розглядають як «чорну скриньку», на вхід якої подаються ресурси X1, X2, …, Xn, а на виході отримуються річні обсяги різноманітної готової продукції Y1, Y2, ..., Yk. Як фактори виробництва на макрорівні здебільшого розглядають виробничі фонди K (капітал) та працю L, а як результати виробництва — валовий випуск продукції (ВВП або НД) Y (рис. 7.1).

Рис. 7.1. Виробнича функція

Отже, економіку моделюють нелінійною ВФ

Y = F(K, L).

Розглянемо найпоширеніші класи ВФ, що застосовуються для моделювання економіки.

ВФ називається неокласичною, якщо вона є гладкою та задовольняє такі умови:

F(0, L) = F(K, 0) = 0 — за відсутності одного з факторів виробництво неможливе;

 — зі зростанням витрат ресурсів виробництво зростає;

 — зі зростанням витрат ресурсів швидкість зростання виробництва спадає;

за необмеженого зростання одного з факторів випуск продук­ції зростає також необмежено.

Мультиплікативна ВФ має такий вигляд (для двох факторів):

де a1, a2 — коефіцієнти еластичності.

Частинним випадком такої ВФ є функція Коба—Дугласа, для якої виконується умова a1 + a2 = 1. Беручи до уваги технологічний прогрес, до моделі часто включають множник exp(lt). Однією з переваг зазначеної моделі є те, що вона стає лінійною після
логарифмування:

,

де індекс t = 1, …, T показує момент часу (або номер спостереження) за факторами виробництва та випуском. Тоді невідомі параметри можна знайти методом найменших квадратів (МНК) за допомогою стандартних пакетів прикладних програм (наприклад, MS Excel, Eviews, SAS тощо).

Можна легко переконатись, що мультиплікативні ВФ задоволь­няють перші дві умови для неокласичних функцій. Справді,
знайдемо перші частинні похідні:

оскільки a1 > 0, a2 > 0.

Частинні похідні випуску за факторами — так звані граничні продукти, або граничні ефективності, факторів — відповідають приросту випуску на одиницю приросту фактора. Неважко переконатись, що мультиплікативна ВФ задовольняє також умови 3 і 4 для неокласичних ВФ.

Подамо економічну інтерпретацію параметрів a1 > 0, a2 > 0. Для цього введемо поняття еластичностей як логарифмічних похідних факторів за випуском:

.

Оскільки в розглядуваному випадку , то

.

Отже, коефіцієнти еластичності показують, на скільки відсотків зросте випуск, якщо фактор зросте на 1 %. При a1 > a2 спостерігається інтенсивне зростання, у протилежному випадку — екстенсивне виробництво.

Ізоквантою називають геометричне місце точок на площині K, L, що відповідає одному й тому самому рівню випуску продукції, тобто F(K, L) = Y0 = const. Звідси випливає, що на
ізокванті

.

Граничною нормою заміни праці фондами та фондів працею називаються відповідно такі співвідношення:

, .

Для мультиплікативної ВФ норма заміни праці фондами прямо пропорційна до фондоозброєності:

Ізоклінами називають лінії найбільшого зростання ВФ. Ізокліни ортогональні до ліній нульового зростання — ізоквант. Оскільки напрям найбільшого зростання задається градієнтом , то рівняння ізоклінали подається у вигляді:

Схематичне зображення ізоквант та ізоклін наведено на
рис. 7.2.

Виробнича функція називається однорідною ступеня g, якщо
F(lK, lL) = lgF(K, L). Отже, мультиплікативна ВФ буде однорідною ступеня a1 + a2.

Розглянемо ще один клас ВФ — зі сталою еластичністю заміни факторів (CES-функції). Для них виконується рівність .

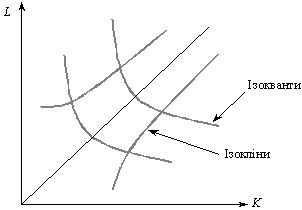
Рис. 7.2. Ізокванти та ізокліни для ВФ

У загальному вигляді ВФ цього класу можна подати так:

,

де .