7.3. Відносні показники варіації
Поряд із абсолютними показниками варіації у статистичній практиці застосовують відносні показники варіації. Вони використовуються:
для оцінки ступеня варіації;
для порівняння варіації різних ознак;
для порівняння варіації однієї ознаки по різних сукупностях.
У загальному вигляді відносні показники варіації визначаються за формулою:
![]()
![]()
Можливі 12 варіантів обчислення Кв:
![]()
![]()
У статистичному аналізі найчастіше використовується коефіцієнт варіації у вигляді:
Вважається, що сукупність є однорідною, якщо V £ 33%. Крім цього, наведений коефіцієнт варіації застосовують для оцінки ступеня варіації:
V < 15% — слабка; 15 £ V £ 25% — середня; V > 25% — сильна.
Наприклад, використаємо коефіцієнт варіації для порівняння варіації успішності студентів у двох групах:
| Оцінка на | Кількість студентів | xf1 | xf2 | x2 | x2f1 | x2f2 | |
| 1 група, f1 | 2 група, f2 | ||||||
| 2 | 3 | 2 | 6 | 4 | 4 | 12 | 8 |
| 3 | 12 | 4 | 36 | 12 | 9 | 108 | 36 |
| 4 | 7 | 11 | 28 | 44 | 16 | 112 | 176 |
| 5 | 2 | 9 | 10 | 45 | 25 | 50 | 225 |
| Разом | 24 | 26 | 80 | 105 | х | 282 | 445 |
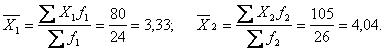
Середній бал по групах:
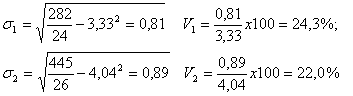
Середні квадратичні відхилення та коефіцієнти варіації по групах:
Отже, у кожній групі має місце досить сильна варіація, причому у першій групі ступінь варіації дещо вищій.
