7.4. Міжгрупова та внутрішньогрупова дисперсії. Правило додавання дисперсій
Чисельні фактори, що обумовлюють варіацію ознаки, можна поділити на дві групи: систематичні та випадкові. Для практичних та наукових потреб необхідно оцінити роль кожної групи факторів у формуванні варіації. При цьому загальну варіацію досліджуваної ознаки необхідно розкласти на дві складові: систематичну та випадкову. Це можна зробити на основі аналітичного групування, при цьому досліджувана ознака є результативною, а групувальна ознака розглядається як систематичний фактор.
Розмір систематичної варіації, яка обумовлюється впливом групувальної ознаки, характеризує міжгрупова дисперсія. Це — середній квадрат відхилень групових середніх значень результативної ознаки (yi) від його загальної середньої (узаг). Таким чином, міжгрупова дисперсія визначається за формулою:
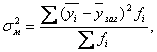
де fi — число одиниць у кожній групі.
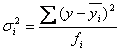
Випадкова варіація обумовлена дією випадкових факторів і проявляється у коливанні значень результативної ознаки в межах однієї групи. Розмір цієї варіації характеризується показником внутрішньогрупової дисперсії. Вона показує середній розмір відхилень значень результативної ознаки (у) від групової середньої (уі) і визначається за формулою:
Внутрішньогрупова дисперсія знаходиться окремо для кожної групи, тому для одержання її значення по сукупності в цілому підраховують середню величину:
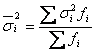
Доведено, що загальна дисперсія результативної ознаки дорівнює сумі міжгрупової дисперсії та середньої з внутрішньогрупових дисперсій:
![]()
Це правило має назву правила додавання дисперсій. Воно використовується для того, щоб розкласти загальну варіацію результативної ознаки на систематичну та випадкову. При цьому мірою систематичної варіації є міжгрупова дисперсія (σм2), а випадкової — середня із внутрішньогрупових дисперсій (σі2).
Розглянемо приклад розрахунку названих дисперсій на прикладі даних про результати екзамену із статистики, при цьому факторною (групувальною) ознакою є стать, а результативною — бал, що одержано на екзамені.
Для одержання розрахункових показників використаємо робочу таблцю:
| Стать | Бали, одержані на екзамені | (у – уі)2 | ||||
| Чоловіки | 3 | 5 | 5 | 1,77 | 0,45 | 0,45 |
| 5 | 4 | 4 | 0,45 | 0,11 | 0,11 | |
| 4 | 3 | 5 | 0,11 | 1,77 | 0,45 | |
| 4 | 5 | 5 | 0,11 | 0,45 | 0,45 | |
| Разом по 1-й групі
|
| |||||
|
|
|
|
|
|
|
| ||||
| Жінки | 3 | 4 | 4 | 0,64 | 0,04 | 0,04 | ||||
|
| 3 | 5 | 3 | 0,64 | 1,44 | 0,64 | ||||
|
| 4 | 5 | 3 | 0,04 | 1,44 | 0,64 | ||||
|
| 4 |
|
| 0,04 |
|
| ||||
|
|
| |||||||||
|
|
| |||||||||
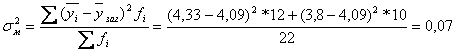
Міжгрупова дисперсія:
Середня з внутрішньогрупових дисперсій:
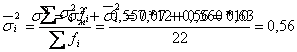
Загальна дисперсія:
Таким чином, варіація оцінок на екзамені із статистики формується переважно за рахунок випадкових факторів, а не під впливом статі студентів.
