8.4. Метод аналітичного групування
Метод аналітичного групування полягає у тому, що сукупність розбивається на групи за факторною ознакою (Х), далі по кожній групі та по сукупності визначаються середні значення Х та Y. Порівняння середній значень факторної та результативної ознак дозволяє зробити певні висновки про наявність та напрямок взаємозв'язку між ними. Крім цього можна визначити показники співвідношення між приростами середніх за формулою:
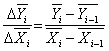 , (6)
, (6)
де ![]()
![]() - середні значення факторної та результативної ознаки по групах (групові середні).
- середні значення факторної та результативної ознаки по групах (групові середні).
Якщо наведене співвідношення по групах приблизно стале, між показниками існую взаємозв'язок.
Для оцінки тісноти взаємозв'язку між ознаками визначається емпіричне кореляційне відношення ![]() :
:
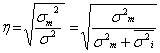 , (7)
, (7)
де ![]() - між групова дисперсія результативної ознаки;
- між групова дисперсія результативної ознаки;
![]() - загальна дисперсія результативної ознаки;
- загальна дисперсія результативної ознаки;
![]() - середня із внутрішньо групових дисперсій результативної ознаки.
- середня із внутрішньо групових дисперсій результативної ознаки.
Емпіричне кореляційне відношення змінюється в межах від 0 до 1. Чим ближче його значення наближається до 1, тим сильнішим є взаємозв'язок між ознаками. При ![]() зв'язок вважається функціональним. Крім цього, визначається коефіцієнт детермінації (D), який показує, на скільки відсотків варіація Y зумовлена варіацією Х:
зв'язок вважається функціональним. Крім цього, визначається коефіцієнт детермінації (D), який показує, на скільки відсотків варіація Y зумовлена варіацією Х:
D = ![]() . (8)
. (8)
Наведемо приклад розрахунку емпіричного кореляційного відношення та коефіцієнту детермінації за результатами аналітичного групування (табл.2)
Таблиця 2
| Групи за факторною ознакою | Кількість одиниць |
|
|
|
| 1 | 15 | 150 | 34 | 14,9 |
| 2 | 25 | 270 | 39 | 15,3 |
| 3 | 40 | 340 | 45 | 13,8 |
| 4 | 12 | 410 | 49 | 18,9 |
| 5 | 8 | 500 | 56 | 25,4 |
| Всього | 100 | х | х | х |
Визначаємо загальне середнє значення результативної ознаки:
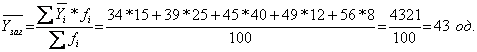
Міжгрупова дисперсія дорівнює:
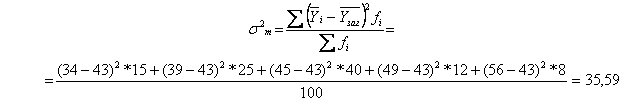
Середня із внутрішньогрупових дисперсій :
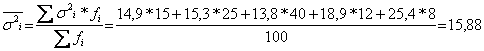
За правилом додавання дисперсій загальна дисперсія результативної ознаки становить:
![]()
Звідси, емпіричне кореляційне відношення :
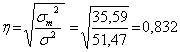
Коефіцієнт детермінації дорівнює:
D= 0,8322 = 0,691 або 69,1%
Отже, між досліджуваними показниками існує сильний прямий зв'язок, а варіація Y на 69,1% обумовлюється варіацією Х.
Крім оцінки тісноти взаємозв'язку необхідно встановити, чи не є відмінність між середніми значеннями Y по групах випадковою (несуттєвою), тобто здійснити перевірку суттєвості зв'язку. Для цього значення ![]() порівнюються з певним критичним значенням, яке знаходиться з спеціальної таблиці, і якщо це відношення більше 1, коливання середніх можна вважати невипадковим, а зв'язок - суттєвим.
порівнюються з певним критичним значенням, яке знаходиться з спеціальної таблиці, і якщо це відношення більше 1, коливання середніх можна вважати невипадковим, а зв'язок - суттєвим.
Для перевірки суттєвості взаємозв'язку між Х та Y часто використовують запропонований Р.Фішером показник, який має назву F-критерія та визначається за формулою :
![]() , (9)
, (9)
де К2 = n-m, K1 = m-1 - число ступеней волі при кількості одиниць n та кількості груп m.
Критичні значення F-критерія для рівнів значимості 0,05 та 0,01 занесені у спеціальні таблиці. Із цих таблиць у відповідності зі значеннями К1 та К2 визначається так зване табличне значення F-критерія (Fтабл). Якщо виконується умова F>Fтабл , зв'язок між показниками можна вважати суттєвим, (невипадковим).
У вищенаведеному прикладі ![]() , К2 = 100-5 = 95, К1 = 5-1 = 4. Табличне значення F-критерія при К1 = 4 (заголовки граф) та К2 = 95 (заголовки рядків) при рівні значимості 0,05 становить 2,5 (Fтабл=2,5). Фактичне значення F-критерія дорівнює:
, К2 = 100-5 = 95, К1 = 5-1 = 4. Табличне значення F-критерія при К1 = 4 (заголовки граф) та К2 = 95 (заголовки рядків) при рівні значимості 0,05 становить 2,5 (Fтабл=2,5). Фактичне значення F-критерія дорівнює:
![]() =
= ![]()
Оскільки F>Fтабл (53,1>2,5), зв'язок між факторною та результативною ознаками є суттєвим, (невипадковим).
