8.5. Парний кореляційно-регресійний аналіз
5. Стохастичні зв'язки, котрі характеризуються взаємодією середніх значень факторної та результативної ознак, називаються кореляційно-регресійними. Такі зв'язки досліджуються з допомогою кореляційно-регресійного аналізу.
Найважливішою характеристикою кореляційного зв'язку є ліній регресії, тобто функція, котра пов'язує середні значення Х та Y . Кореляційно-регресійна модель взаємозв'язку являє собою рівняння регресії, яке у загальному вигляді записується наступним чином:
![]() , (10)
, (10)
де ух – теоретичні значення Y ;
![]() - лінія регресії;
- лінія регресії;
![]() - залишкова компонента.
- залишкова компонента.
У парному кореляційно-регресійному аналізі переважно використовуються наступні функції (рівняння регресії):
лінійна ![]()
параболічна ![]()
кубічна ![]()
степенева ![]()
гіперболічна ![]() .
.
Розглянемо методику кореляційно-регресійного аналізу на прикладі лінійного зв'язку, який описується лінійним рівнянням регресії. На першому етапі доцільно застосувати графічний метод для формування гіпотези про наявність саме лінійного взаємозв'язку між ознаками.
На другому етапі визначаються параметри лінійного рівняння регресії:
![]() .
.
Для цього використовується метод найменших квадратів та розв'язується система рівнянь відносно а0 і а1 :
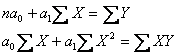
![]()
З наведеної системи параметри рівняння регресії розраховуються різними способами, в тому числі за формулами:
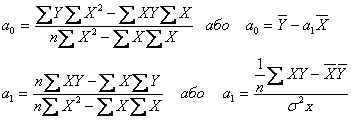
Параметри а0 і а1 мають певний економічний зміст, зокрема, а1 називається коефіцієнтом регресії, що показує, на скільки одиниць змінюється Y при збільшенні Х на одну одиницю. Якщо цей коефіцієнт додатний – зв'язок прямий, а якщо від'ємний – зв'язок між показниками обернений.
На третьому етапі за одержаним рівнянням регресії розраховуються теоретичні значення результативної ознаки Yх та показники рівня апроксимації (наближення), які показують розбіжність між фактичними і теоретичними значеннями Y :
середня квадратична (стандартна) помилка:
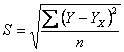 (11)
(11)
коефіцієнт апроксимації:
![]() . (12)
. (12)
Чим меншими є значення S та V, тим краще рівняння регресії описує (апроксимує) взаємозв'язок між Х та Y .
На четвертому етапі оцінюється тіснота зв'язку за допомогою лінійного коефіцієнта кореляції (r):
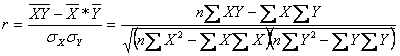 . (13)
. (13)
Значення коефіцієнта кореляції r знаходиться в межах від -1 до +1. При r>0 зв'язок між показниками прямий, а при r<0 – обернений. Якщо : ![]() вважається, що зв'язок між Х та Y практично відсутній;
вважається, що зв'язок між Х та Y практично відсутній; ![]() - зв'язок слабкий;
- зв'язок слабкий; ![]() - зв'язок середній;
- зв'язок середній; ![]() - зв'язок сильний;
- зв'язок сильний; ![]() - зв'язок дуже сильний.
- зв'язок дуже сильний.
Коефіцієнт детермінації D=r2 показує, на скільки відсотків варіація Y обумовлюється варіацією Х.
Часто також визначається коефіцієнт еластичності (Е) за формулою:
Е=![]() . (14)
. (14)
Цей коефіцієнт показує, на скільки процентів змінюється Y при збільшенні Х на 1%.
На п'ятому етапі здійснюється перевірка суттєвості (невипадковості) взаємозв'язку між показниками за допомогою F-критерія Фішера:
F=![]() , (15)
, (15)
де К1=m-1; K2=n-m; n – кількість одиниць у сукупності; m - кількість параметрів у рівнянні регресії.
Розглянемо приклад розрахунків вищенаведених показників, використовуючи робочу таблицю 3.
Таблиця 3
| Ціна,грн. (Х) | Обсяг продажу, шт. ( Y ) |
ХY |
Х2 |
Y2 |
Yх |
(Y –Yх )2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2,0 | 120 | 240,0 | 4,00 | 14400 | 120 | 0 |
| 2,4 | 88 | 212,2 | 5,76 | 7744 | 82 | 36 |
| ... | … | … | … | … | … | … |
| 25,0 | 730 | 1755,7 | 63,24 | 60214 | 731 | 420 |
Визначаємо параметри лінійного рівняння регресії:
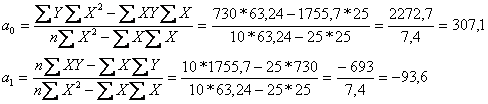
Отже, лінійне рівняння регресії має вигляд:
Yх = 307,1 - 93,6Х .
Таким чином, при збільшенні ціни на 1 грн. Обсяг продажу в середньому зменшується на 93,6 од.
Теоретичні значення Y (Yх ) визначаються шляхом підстановки у рівняння регресії значень Х:
Yх1=307,1 – 93,6*2,0 = 120
Yх2=307,1 – 93,6*2,4 = 82 і т.д.
Теоретичні значення Y занесені у 6 графу таблиці 3.
Визначаємо середню квадратичну (стандартну) помилку та коефіцієнт апроксимації:
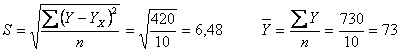
![]() .
.
Для оцінки тісноти взаємозв'язку між ознаками підрахуємо лінійний коефіцієнт кореляції:
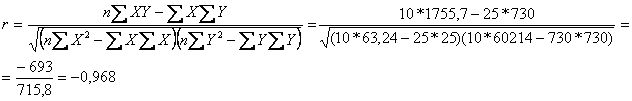
Таким чином, між ознаками існує дуже тісний кореляційний зв'язок. Коефіцієнт детермінації (D=r2=-0,9682=0,937) показує, що варіація Y на 93,7% зумовлена варіацією Х. Коефіцієнт еластичності
Е=![]() .
.
Отже, при збільшенні ціни на 1% обсяг продажу зменшується на 3,2%.
Далі здійснюється перевірка суттєвості зв'язку за допомогою F-критерія Фішера:
F=![]()
Табличне значення F-критерія при рівні значимості 0,05 та числі ступенів волі 8 і 1 дорівнює 5,3. Таким чином, F>Fтабл (119,9>5,3), а зв'язок між ознаками невипадковий (суттєвий).
