10.3. Методи обробки рядів динаміки
У статистичній практиці не завжди можна обмежитися визначенням аналітичних показників ряду динаміки. Для всебічного аналізу закономірностей динаміки необхідно використовувати різноманітні методи обробки рядів з метою виділення їх загальної тенденції (тренду).
Для порівняння швидкості зміни двох або більше взаємопов’язаних показників використовують метод приведення рядів динаміки до єдиної основи. Суть цього методу полягає у тому, що вихідні ряди динаміки абсолютних значень показників замінюються базисними темпами зростання, котрі визначені відносно однакового моменту ( періоду) часу. Порівняння базисних величин дозволяє зробити висновок про те, який з показників зростає або зменшується швидше.
Приклад розрахунку:
| Місяці | 1 | 2 | 3 | 4 | 5 | 6 |
| Витрати на виробництво, тис. грн. | 10,7 | 12,4 | 15,1 | 14,9 | 16,2 | 15,8 |
| Прибуток, тис. грн. | 3,1 | 3,2 | 3,5 | 3,7 | 3,6 | 6,4 |
| Базисні темпи зростання, % |
|
|
|
|
|
|
| витрат | 100 | 115,9 | 141,1 | 139,3 | 151,4 | 147,7 |
| прибутку | 100 | 103,2 | 112,9 | 119,4 | 116,1 | 206,5 |
Для виявлення тенденції зміни показника у досить довгих рядах динаміки використовують метод збільшення інтервалів часу. При цьому вихідні рівні ряду замінюють сумарними або середніми значеннями показника за більші періоди часу. Наприклад, відомі дані про щомісячний обсяг продажу товару, шт.
| Місяці | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| y | 700 | 692 | 698 | 704 | 690 | 686 | 671 | 682 | 665 | 640 | 661 | 654 |
Використаємо метод збільшення інтервалів часу та визначимо середній обсяг продажу по кварталах:
| І квартал |
|
| ІІ квартал |
|
| ІІІ квартал |
|
| ІV квартал |
|
Отже, спостерігається чітко визначена тенденція до зменшення обсягу продажу на протязі року.
Для обробки ряду динаміки з метою зменшення коливань його рівнів використовується метод рухомої середньої. Суть цього методу полягає у тому, що первинний ряд динаміки замінюється рядом середніх значень, підрахованих на основі рухомих сум. Рухома сума визначається шляхом додавання рівнів ряду, включених в інтервал вирівнювання (переважно це 3, 5, 7 рівнів).
Приклад розрахунку:
| Місяці | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 700 | 692 | 698 | 704 | 690 | 686 | 671 | 682 | 665 | 640 |
| Рухомі суми | — | 2090 | 2094 | 2092 | 2080 | 2047 | 2039 | 2018 | 1987 | — |
| Рухомі середні | — | 697 | 698 | 697 | 693 | 682 | 680 | 673 | 662 | — |
Головним недоліком даного методу є те, що вирівняний ряд стає коротшим від вихідного за рахунок втрати рівнів на початку та в кінці ряду.
Найбільш ефективним методом виявлення тенденції динаміки є аналітичне вирівнювання. Його суть полягає у тому, що вихідний ряд динаміки описують рівнянням тренду, яке розглядається як аналітичний вираз загальної тенденції зміни у часі (тренду). На практиці найчастіше використовують наступні рівняння тренду:
| — лінійне |
|
| — параболічне |
|
| — показникове |
|
| — степеневе |
|
| — гіперболічне |
|
Розглянемо техніку виконання аналітичного вирівнювання на прикладі лінійного рівняння тренду. Параметри а0 та а1 знаходяться з системи нормальних рівнянь методом найменших квадратів. Для спрощення підрахунків параметр часу t задаються таким чином, щоб ![]() . Тоді
. Тоді
![]()
Параметр а1 показує, на скільки одиниць в середньому змінюється показник за одиницю часу. Вирівняні (розрахункові) значення одержуються шляхом підстановки в одержане рівняння тренду заданих значень t .
Приклад розрахунку:
| Місяці | 1 | 2 | 3 | 4 | 5 | Разом |
| y | 210 | 217 | 225 | 237 | 244 | 1133 |
| t | - 2 | - 1 | 0 | 1 | 2 | 0 |
| yt | - 420 | -217 | 0 | 237 | 488 | 88 |
| t2 | 4 | 1 | 0 | 1 | 4 | 10 |
| yt | 209 | 218 | 227 | 235 | 244 | 1133 |
Визначимо параметри лінійного рівняння тренду:
![]() .
.
Отже, рівняння тренду має вигляд:
![]() .
.
Розрахункові значення:
![]()
Таким чином, в середньому за місяць показник зростає на 8,8 од.
Для перевірки адекватності моделі (рівняння тренду) використовують наступні показники:
- середнє квадратичне (стандартне) відхилення
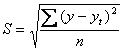 ;
;
- коефіцієнт апроксимації
![]() .
.
Вважають, що рівняння тренду достатньою мірою апроксимує (описує) ряд динаміки, якщо V<10%.
Визначимо показники рівня апроксимації для раніше наведеного рівняння тренду:
| Місяці | 1 | 2 | 3 | 4 | 5 | Разом |
| y | 210 | 217 | 225 | 237 | 244 | 1133 |
| yt | 209 | 218 | 227 | 235 | 244 | 1133 |
|
| 1 | 1 | 4 | 4 | 0 | 10 |
![]() ,
, ![]()
Отже, лінійне рівняння тренду дуже добре описує вихідний ряд динаміки.
