11.2. Елементи теорії лінійних операторів

11.2. Елементи теорії лінійних операторів

Основну формулу теорії регулювання y = (S / 1 – SR)x було виведено за умови, що S і R є операторами пропорційного перетворення, яке відбувається відповідно в регульованій системі та в регуляторі, тобто в обох системах відбуваються перетворення, що полягають у множенні стану входу на дійсні числа S і R. Покажемо тепер, що основна формула теорії регулювання має значно ширший спектр застосування. Зокрема, умова про здійснення тільки пропорційного перетворення може бути замінена більш загальною передумовою. З цією метою розглянемо основні положення операторного числення.

Процес перетворення стану входу х системи на стан виходу у можна записати в термінах відображень:

або у = Тх.

Символ Т називається оператором перетворення, який визначає, що необхідно зробити зі станом х на вході, щоб одержати стан у на виході. Сукупність правил виконання алгебраїчних дій над операторами називається операторним численням.

Розглянемо найпростіший клас операторів — лінійні оператори. Це оператори, що задовольняють такі дві умови:

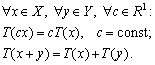
Перша з цих умов означає, що перетворення Т величини сх (де с = const) рівнозначне перетворенню Т величини х з подальшим множенням результату на сталу с, а отже, цю сталу можна винести за знак оператора.

Інша умова означає, що лінійні оператори мають властивість адитивності — перетворення суми величин х і y рівнозначне сумі того самого перетворення величини х і величини y.

Найпростіший лінійний оператор — оператор пропорційного перетворення, який перетворює стан входу х на стан виходу у за допомогою множення стану входу на деяке дійсне число: y = kx, де k = const. Стала k називається коефіцієнтом перетворення. Зауважимо, що стала k не є оператором пропорційного перетворення, оскільки в даному разі оператор — це правило: «помножити х на k».

До основних лінійних операторів належать:

1. Оператор пропорційного перетворення або оператор пропорційності. Його дія полягає у множенні стану входу х на стале дійсне число.

2. Оператор диференціювання. Якщо стан входу х є непе-
рервною функцією деякого параметра t, тобто x =  f(t), то цей оператор означає, що для досягнення визначеного стану виходу необхідно продиференціювати функцію f(t), тобто визначити похід­ну цієї функції. Оператор диференціювання позначається d / dt
або символом D. З диференціального числення відомо, що при відшуканні похідної виконуються умови лінійності перетворення, оскільки Dcx =  cDx і D(x + у) =  Dx + Dу.

3. Оператор (невизначеного) інтегрування, дія якого полягає в тому, що стан виходу визначається як первісна (інтеграл) стану входу x = f(t). Цей оператор позначається символом невизначеного інтеграла (чи символом D1, оскільки інтегрування є оператором, оберненим до диференціювання). Це лінійний оператор, оскільки сталу можна винести за знак інтеграла, і, крім того, інтеграл суми дорівнює сумі інтегралів.

4. Різницевий оператор, який позначається символом D. Його дія полягає ось у чому. Якщо множину можливих значень станів входу системи можна подати у вигляді ряду х1, х2, ..., хп, то оператор D перетворить стан входу хi на різницю хi+1 – хi, або Dхi =  хi+1 – хi. Цей оператор також є лінійним, оскільки

Dcxi =  cxi+1 – cxi =  c(хi+1 – хi) =  cDхi ;

D(хi + уi) =  хi+1 + уi+1 – хi – уi =  Dхi + Dуi .

5. Оператор підсумовування позначається символом å. Його дія полягає в підсумовуванні станів входу за деяким індексом i.

6. Оператор правого зсуву (випередження), що позначається символом Е. Якщо множину можливих значень входу системи можна подати у вигляді ряду х1, х2, ..., хп, то оператор Е перетворить стан входу хi на стан виходу у = xi+1 . Отже, Eхi =  хi+1.

7. Оператор лівого зсуву (запізнювання) аналогічний оператору випередження, але стан входу хi тут перетвориться в стан виходу xi–1. Якщо позначити його через Е–1, то E–1хi =  хi–1. Неваж­ко переконатися, що три останніх оператори також лінійні.

У техніці ці оператори мають такі відповідно назви: пропорційний перетворювач (залежно від призначення — підсилювач чи послаблювач), диференціатор, інтегратор, пристрій виперед­ження чи затримки.

Розглянемо основні алгебраїчні дії, які можна виконувати з операторами перетворення.

Сумою двох операторів називається вираз:

(Т1 + Т2)х = Т1х + T2x.

Це означає, що сума операторів T1 і Т2, застосованих до х, приводить до того самого результату, що й застосування до х спочатку оператора T1, а потім оператора Т2 з наступним додаванням здобутих результатів. Аналогічно визначається різниця двох операторів.

Добуток двох операторів визначається рівністю:

T2 T1x =  T2 (T1x),

яка означає, що застосування до х добутку операторів Т1 і Т2 полягає в послідовному перетворенні х за допомогою T1, а потім — у перетворенні здобутого результату оператором T2.

Зауважимо, що добуток операторів не обов’язково є комутатив­ним. Тому перетворення х спочатку за допомогою оператора T1, а потім за допомогою оператора Т2 може дати інший результат, ніж перетворення, виконані у зворотному порядку.

За означенням n-а степінь оператора Тn, де п — натуральне число, є n-кратний добуток (повторення) того самого перетворення:

Tnx = T(Tn–1 x).

Символом Т–1 позначається обернений оператор. Зміст цього оператора полягає в тому, що коли Т є оператором перетворення х на у, то Т–1 є оператором перетворення у на х: якщо y = Тх, то
х =  Т–1у.

Визначення оператора Т–1 дає змогу подати відношення операторів:

Введемо поняття тотожного перетворення, оператор якого позначимо через Т0 або через І. У разі тотожного перетворення величина х перетворюється на ту ж величину х: Т0 =  Іх =  х. Якщо
перетворення пропорційне, то І є оператором перетворення, дія якого полягає у множенні на 1 (І = 1).

З означення оберненого оператора випливає, що

Т Т–1 = Т–1Т = Т0 = І.

Означені щойно дії з операторами дають змогу одні з розглянутих основних лінійних операторів виражати через інші. Наприклад, оператор (невизначеного) інтегрування можна замінити оператором, оберненим до оператора диференціювання; оператор випередження тотожний оператору, оберненому до оператора запізнювання тощо.

Різницевий оператор D можна подати за допомогою оператора випередження Е. Справді:

Dхi = xі+1 – xі = Exi – xi = (E – 1)xi

і, отже, D º Е – 1 (різницевий оператор тотожний різниці між оператором випередження та оператором тотожного перетворення).

Оператор підсумовування також можна подати за допомогою оператора випередження:

.

Отже, сім основних лінійних операторів можна подати за допомогою комбінації лише трьох елементарних лінійних операторів: оператора пропорційності, оператора диференціювання та оператора правого зсуву (випередження).

Доведемо тепер, що основна формула теорії регулювання справджується для будь-яких перетворень, що відбуваються в регульованій системі та у регуляторі (за умови лінійності операторів).

Припустимо, що в регульованій системі відбувається довільне перетворення y = Sx, де оператор перетворення S є лінійним. У регуляторі за допомогою зворотного зв’язку до системи підім­кнено регулятор, в якому відбувається перетворення Dx = Ry, де R — також довільний лінійний оператор. Отже, дістанемо систему регулювання, в якій відбувається таке перетворення:

у =  S (х + Dx) = S (х + Ry).

Оскільки оператори S і R лінійні, то виконується співвідношення

у =  S (х + Ry) =  Sx + SRy,  y – SRy =  Sx.

Звідси випливає, що (I – SR)y =  Sx, і, оскільки I = 1, дістанемо основну формулу теорії регулювання:

,

яка виконується, якщо оператори лінійні.

Таким чином, операторне числення є дуже зручним засобом дослідження систем регулювання, адже над операторами можна виконувати алгебраїчні дії та діставати формули за аналогією з діями над числами.