15.1. Принцип підпорядкування Хакена та параметри порядку

15.1. Принцип підпорядкування Хакена та параметри порядку

Дослідники, аналізуючи функціонування макроекономіки, економіки регіону, сектора, галузі чи підприємства й намагаючись урахувати численні фактори та взаємозв’язки, часто змушені будувати математичні моделі (системи) великої розмірності, що містять десятки або й сотні параметрів і рівнянь. Аналітичний аналіз таких моделей доволі складний і становить окрему проблему, а через це їх важко застосовувати на практиці та інтерпретувати здобувані результати.

Проте існує спосіб редукції відповідних систем до систем рівнянь значно меншої розмірності, завдяки чому вдається подати якісний опис об’єкта за допомогою кількох диференціальних рівнянь. Ідея цього методу полягає в тому, що коли йдеться про опис динаміки системи, не всі її параметри (або процеси, які вони характеризують) мають однакові часові масштаби зміни. Деякі параметри стану (швидкі змінні) можна виразити через інші (повільні змінні) — так звані параметри порядку, у результаті чого кількість незалежних змінних зменшується. Можливість подати швидкі змінні як функції параметрів порядку становить зміст принципу підпорядкування Хакена. Але варто зауважити, що задовго до Хакена цей метод був запропонований О. Тихоновим і відомий як теорема Тихонова. Розглянемо, у чому полягає її ідея.

Розглянемо процес спрощення моделі у вигляді системи n автономних нелінійних диференціальних рівнянь [2]:

.

Нехай після деяких перетворень систему можна впорядкувати за малим параметром при похідній, тобто подати у вигляді:

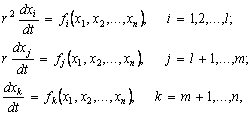
де r — малий параметр (r < 1).

Щоб досліджувати поводження системи на короткострокових (порядку r2) і на довгострокових (порядку 1) часових інтервалах, необхідно розглядати повну систему. А коли йдеться про поводження системи на середньострокових часових інтервалах (порядку r), то її рівняння з параметром r2 описують досить швидкі процеси, а рівняння з параметром 1, навпаки — досить повільні. Тому можна вважати, що за час T ¥ r змінні xk не зазнають істотних змін, а отже, у рівняннях, що залишилися, ці повільні змінні можна замінити їх початковими значеннями, знизивши розмірність системи на n – (l + m). Діючи так і далі, ми можемо зредуціювати вихідну систему до системи розмірністю l.

Параметри порядку й принцип підпорядкування належать до числа найбільш фундаментальних понять синергетики. З економічного погляду принцип підпорядкування означає, що можна знайти невелику кількість змінних (можливо, агрегованих, перетворених тощо), які визначають динаміку всієї економічної системи в околі особливої точки, а решта змінних залежить від них.