4.1. Основні лінії та площини еліпсоїда

Положення точок на земній поверхні та на поверхні еліпсоїда визна­чаються їх координатами в тій чи іншій системі.

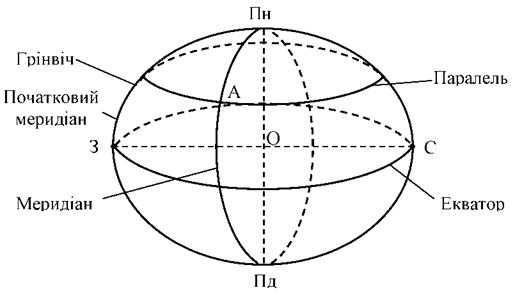
Координатами називають лінії та кутові величини, що визначають по­ложення точки в тій чи іншій системі. Осями координат і координатними площинами називають лінії та площини, відповідно до яких визначають поло­ження точок. Для визначення місцеположення точок і напрямків використо­вують характерні лінії і площини на поверхні еліпсоїда обертання (рис. 4.1).

Площина екватора - площина, що перпендикулярна до осі обертан­ня еліпсоїда і проходить через його центр.

Екватор - лінія перетину еліпсоїда площиною, що проходить через центр еліпсоїда і перпендикулярна до його осі обертання, тобто до поляр­ної площини. Екватор - є коло, радіус якого дорівнює великій півосі.

Паралелі - лінії перетину поверхні еліпсоїда площинами, що пара­лельні площині екватора. Вони являють собою кола.

Меридіан - лінія перетину земного еліпсоїда меридіальною площиною. Будь-який меридіан - це еліпс, який своїм обертанням навколо малої осі утворює еліпсоїд.

Нормаль до поверхні еліпсоїда в даній точці (рис. 4.2) є пряма, що перпендикулярна до площини, яка дотична до еліпсоїда в цій точці. Нор­маль до поверхні еліпсоїда завжди лежить в меридіальній площині, що проходить через дану точку. Для точок північної половини еліпсоїда пара­лелі перетинають вісь на північ від центра еліпсоїда, а для точок південної

Довжина паралелі визначається відрізком нормалі від поверхні еліп­соїда до його малої осі. Нормальними площинами називаються всі площи­ни, що проходять через нормаль. Нормальний переріз - це є лінії перетину нормальних площин з поверхнею еліпсоїда.

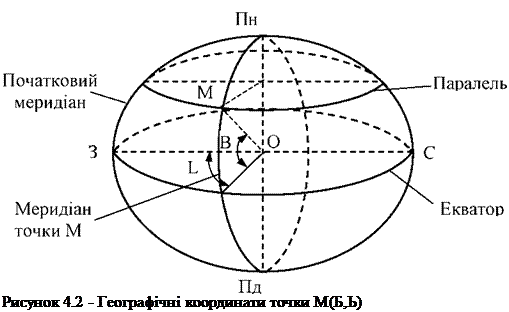Прямовисна лінія - напрямок вектора сили тяжіння в даній точці. Пря­мовисна лінія перпендикулярна дотичній до поверхні геоїда в даній точці.