4.2. Ентропія та інформація
4.2. Ентропія та інформація
Щойно ентропію було розглянуто як міру невизначеності системи. Зрозуміло, що з появою нових відомостей невизначеність може зменшитися. Чим більший обсяг зазначених відомостей, тим більше буде інформації про систему і тим менш невизначеним буде її стан. Тому кількість інформації можна вимірювати зменшенням ентропії тієї системи, для уточнення стану якої призначено відомості.
Розглянемо деяку систему Х, щодо якої виконуються спостереження, і оцінимо інформацію, здобуту в результаті того, що стан системи став цілком відомим. До отримання відомостей ентропія системи була Н(Х), а коли їх було отримано, стан системи цілком визначився, тобто ентропія стала дорівнювати нулю. Нехай Ix — інформація, здобута в результаті з’ясування стану системи Х. Вона дорівнює зменшенню ентропії:
![]() , (4.6)
, (4.6)
тобто кількість здобуваної інформації в разі повного з’ясування стану деякої фізичної системи дорівнює ентропії цієї системи. Формулу (4.6) можна записати докладніше:
![]() , (4.7)
, (4.7)
де Pi = P(X = xi). Співвідношення (4.7) означає, що інформація Ix є усередненим (за всіма станами системи) значенням логарифма ймовірності стану (зі знаком «мінус»). Кожний окремий доданок
(–logPi) можна розглядати як часткову інформацію від окремого повідомлення, яке полягає в тому, що система Х перебуває у стані хi. Позначивши цю інформацію через ![]() , дістанемо:
, дістанемо:
![]() . (4.8)
. (4.8)
Тоді інформація Ix буде середньою (повною) інформацією, що її було отримано від усіх можливих окремих повідомлень:
![]() , (4.9)
, (4.9)
де Х —кожний (випадковий) стан системи Х.
Оскільки 0 £ Pi £ 1, то як часткова Ix, так і повна Ix невід’ємні. Якщо всі можливі стани рівноможливі (P1 = P2 = … = Pn = 1/n), то
![]() ,
, ![]()
Ми розглядали інформацію про стан деякої системи Х, отриману за допомогою безпосереднього її спостереження. На практиці система Х найчастіше буває недоступна безпосередньому спостереженню, і стан її з’ясовується за допомогою деякої системи Y, певним чином пов’язаної з нею. Наприклад, замість безпосереднього спостереження за літаком ведеться спостереження за екраном локатора і т. ін.
Розбіжності між системою Х, яка нас безпосередньо цікавить, і спостережуваною системою Y можуть бути двох типів.
1. Розходження за рахунок того, що система Y «грубіша», менш різноманітна, є гомоморфним образом Х, тому деякі стани Х не відображуються в Y.
2. Розбіжності за рахунок помилок: неточностей вимірювання параметрів системи Х і помилок у передаванні повідомлень.
У разі, коли зазначені системи Х та Y різні, постає запитання: яку кількість інформації про систему Х дасть спостереження над системою Y?
Природно визначити цю інформацію як зменшення ентропії системи Х в результаті отримання відомостей про стан системи Y:
![]() . (4.10)
. (4.10)
Справді, доти, доки відомостей про систему Y не було, ентропія системи Х становила Н(Х). Після отримання відомостей «залишкова» ентропія стала Н(Х/Y). Отож знищена відомостями ентропія і є інформація ІY®X.
Величину ІY®X називають повною, або середньою, інформацією про систему Х, що міститься в системі Y.
Можна довести, що ІY®X = ІX®Y. Позначимо через ІX«Y =
= ІX®Y = ІY®X. Інформацію ІX«Y називають повною взаємною інформацією, що міститься в системах Х та Y.
Якщо системи незалежні, то Н(Х / Y) = Н(Х) і ІX«Y = 0, тобто повна взаємна інформація, що міститься в незалежних системах, дорівнює нулю. Це природно, оскільки неможливо дістати відомості про систему, спостерігаючи замість неї іншу, з нею не пов’язану.
Розглянемо випадок, коли стан системи Х цілком визначає стан системи Y. Тоді Н(Х / Y) = 0 і, навпаки, Н(Y / Х) = 0, тобто системи еквіваленті:
![]() . (4.11)
. (4.11)
Якщо між системами Х та Y існує зв’язок, причому Х — більш різноманітна, ніж Y, причому Н(Х / Y) = 0, тоді
ІX«Y = Н(Y) – Н(Y / Х) = Н(Y),
тобто повна взаємна інформація ІX«Y, що міститься в системах, одна з яких є підлеглою, дорівнює ентропії підлеглої системи.
Виведемо формулу для інформації. З огляду на те, що
Н(Y / Х) = Н(Х / Y) – Н(Y),
дістанемо:
ІX«Y = Н(Х) – Н(Х / Y) = Н(Х) + Н(Y) – Н(Х, Y). (4.12)
Отже, повна взаємна інформація, що міститься у двох системах, дорівнює сумі ентропії обох систем, що становлять систему, за винятком ентропії системи, утвореної перерізом даних систем.
Графічно це можна зобразити так, як показано на рис. 4.1.
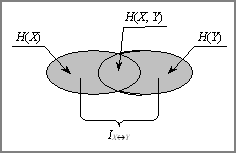
Рис. 4.1. До визначення повної взаємної інформації
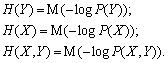
Звідси, можемо записати:
![]()
![]() ,
,
де Pij = P(X = xi; Y = yj), pi = P(X = xi) rj = P(Y = yj).
