15.3. Дискретні відображення

15.3. Дискретні відображення

Якщо стан системи характеризується однією змінною x, тобто розмірність фазового простору дорівнює одиниці, а оператор еволюції задається рекурентним співвідношенням:

,    (15.1)

де n — дискретний час;  — неперервне відображення замкненого інтервалу J дійсної числової прямої в себе, то таке співвідношення називають одновимірним дискретним відображенням.

Точку  називають невиродженою періодичною точкою з періодом k, якщо  де  — k-та ітерація
f-орбітою.

І хоча вираз (15.1) на перший погляд здається надто простим, такі відображення доволі корисні під час аналізу складних систем. Розглянемо кілька типових ситуацій, коли доводиться використовувати дискретні відображення як математичні моделі динамічних процесів [6].

Відображення як моделі процесів із дискретним часом. або коли ми маємо Ідеться про спостереження за процесом у дискретні моменти часу n = 1, 2, 3, …, а отже, у такому разі природно вважати змінну x(n), або як її часто позначають xn, дискретною Скажімо, числові значення багатьох економічних змінних (ВВП, індекси цін, обсяги зовнішньої торгівлі тощо) вдається знайти, як правило, у певні дискретні моменти часу.

Відображення, що виникають у результаті застосування методу Ейлера до розв’язування диференціальнихх рівнянь. Розглянемо, наприклад, модифіковану модель Мальтуса, яка описує динаміку чисельності населення (популяції):

,

що пропорційна кількості населення N. Якщо  то
N(t) ® 1 при t ® ¥. Застосувавши до цього рівняння метод
Ейлера, після заміни змінних дістанемо дискретне відобра-
ження:

.

Відображення, що виникають у процесі чисельного розв’язуванні нелінійних алгебраїчних рівнянь. Так, розв’язуючи рівняння виду x = F(x), будують послідовність , яка збігається до кореня . Це можна зробити методом простої ітерації, згідно з яким , або методом Ньютона: .

В обох випадках дістаємо дискретні відображення.

Побудова відображень як метод обробки експерименталь­них даних. Нехай ми спостерігаємо перебіг деякого складно-
го процесу x(t). Позначимо його локальні максимуми через Mk. На площині  відкладатимемо точки з координатами , тобто перша точка буде , друга  і т. д. Як з’ясувалося для багатьох процесів точки  з високою точністю належать однозначним неперервним кривим . Існування такої функції f дає змогу в деяких випадках будувати прості моделі, за допомогою яких за попередніми локальними максимумами вдається знаходити наступні, прогнозуючи характер та поводження досліджуваного процесу.

Для одновимірних неперервних відображень здобуто кілька цікавих результатів. Передусім це теорема Шарковського та її частинний випадок, який дослідили американські математики Лі та Йорке [4; 5]. Так, згідно з результатами Лі та Йорке, якщо  відображення (15.1) має цикл періоду 3, то воно має нескінченну множину циклів решти періодів і нескінченну множину хаотичних траєкторій. Єдина вимога, що накладається на функцію f(x), — це її неперервність. Отже, навіть прості системи можуть поводитися хаотично.

Цей результат є частковим випадком теореми Шарковсь-
кого.

Якщо неперервне відображення одновимірного інтервалу в себе має цикл періоду m, то воно має також усі можливі цикли періоду k, що передують числу m у переліку всіх цілих чисел, записаних у так званому порядку Шарковського:

Найцікавішим для економічного аналізу є так зване логістичне відображення:

.

Завдяки аналізу логістичного відображення було з’ясовано багато спільних властивостей одновимірних відображень, зокрема так званий сценарій переходу до хаосу Фейгенбаума. Щоб розкрити його суть, побудуємо графік  (біфуркаційну діаграму). На осі x відкладатимемо значення , що містяться на стійкому цик­лі або на іншому атракторі, а по осі  — значення параметра
(рис. 15.2). Циклу порядку 2 відповідатимуть дві точки на одній вер­тикалі, порядку 4 — чотири точки і т. д. Позначимо через
 значення параметра, при яких відбуваються подвоєння, а через  значення параметра, при яких точка x = 0,5 є елементом циклу порядку два, чотири і т. д. Нехай d1, d2 … — відстані між прямою x = 0,5 та найближчою точкою відповідного циклу.

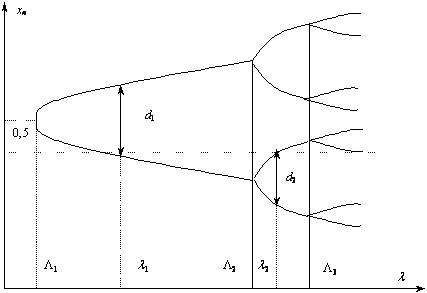
Рис. 15.2. Біфуркаційна діаграма для логістичного відображення

Фейгенбаум показав, що значення точок біфуркації  прямує до границі:

.

При цьому відношення dn /dn+1 також прямує до границі, яка дорівнює — 2,5029... .

Ще один висновок полягає в тому, що відношення довжин суміжних інтервалів між біфуркаціями також прямують до границі:

.

Константу d називають сталою Фейгенбаума та використовують для прогнозування досягнення області хаосу. Можна показати, що інтервал між приблизно дорівнює .

Сценарій виникнення неперіодичного руху, хаотичного атрактора в результаті біфуркацій подвійного періоду спочатку було досліджено для логістичного відображення. Пізніше було здобуто строгі результати, що дозволяють виявляти класи одновимірних відображень, для яких перехід до хаосу характеризується сценарієм Фейгенбаума.

Але експериментальні дослідження та комп’ютерне моделювання багатьох нелінійних систем показали, що їм притаманна послідовність біфуркацій подвійного періоду, а значення біфуркаційних параметрів і амплітуди циклів характеризуються тими самими універсальними константами. При цьому досліджувані явища можуть описуватися багатовимірними відображеннями, автономними або неавтономними системами звичайних диференці-
альних рівнянь або рівняннями в частинних похідних. Отже, широ­кий клас нелінійних явищ не тільки демонструє однакову якісну поведінку, а й має універсальні кількісні характеристики.