10.3. Моделі управління грошовими коштами

10.3. Моделі управління грошовими коштами

Модель управління грошовими коштами Баумола

На практиці виникає проблема визначення оптимальної суми потрібних грошових коштів. Із цією метою використовуються моделі управління грошовими коштами. Ознайомимося з моделлю американського економіста Уільямса Баумола (Baumol). Як і будь-яка економічна модель, модель Баумола передбачає ряд спрощень. Корпорація функціонує в стабільному фінансовому середовищі, її грошові потоки стабільні і цілком передбачувані.

Приклад. Припустимо, корпорація виплачує щотижня за своїми рахунками 100 000 ф. ст., приплив грошових коштів становить 80 000 ф. ст. Таким чином, щотижня потрібна додаткова сума в 20 000 ф. ст. Одержувані кошти (80 000 ф. ст.) корпорація витратить за чотири тижні для покриття від’ємного сальдо, до кінця четвертого тижня залишок грошових коштів зводиться до нуля. Отже, корпорація повинна відновлювати початковий залишок у 80 000 ф. ст. через продаж цінних паперів зі свого портфеля або одержання позички в комерційному банку (рис. 10.2, 10.3). Проте ці операції пов’язані з операційними витратами, припустимо, що вони становлять 500 ф. ст.

Рис. 10.2. Сальдо грошових коштів відповідно до моделі Баумола[1]

Середній залишок грошових коштів становить 40 000 ф. ст. (Q/2). Завдання, поставлене перед менеджером корпорації, полягає в тому, щоб визначити найбільш прийнятну суму грошових коштів. Її підвищення до 120 000 ф. ст. і середнього сальдо до 60 000 ф. ст. означало б підвищення витрат невикористаних можливостей, наприклад, дохід, який можна було б одержати з легко реалізованих цінних паперів. З іншого боку, менеджер повинен враховувати операційні витрати.

За моделлю Баумола виділяються такі чинники для визначення оптимального залишку грошових коштів:

Q — максимальний залишок;

Q/2 — середній залишок;

С — операційні витрати, пов’язані з продажем цінних паперів із портфеля корпорації або з одержанням банківської позички;

А — загальна сума нових надходжень грошових коштів, яка необхідна на певний період, звичайно на один рік;

K — вартість невикористаних можливостей (opportunity cost — «ціна шансу»), тобто можливості одержання більш високого процентного доходу.

Таким чином, виводиться перша формула:

.

З неї виводиться формула, за якою визначається оптимальний грошовий залишок Q*:

.

За умови, що K = 7 %, річні потреби в грошових коштах
А = 1 040 000 ф. ст. (20 000 · 52 тижні), С = 500 ф. ст. (див. с. 379), оптимальний залишок (сальдо) грошових коштів становитиме:

Отже, буде потрібно 121 890 ф. ст. для поповнення грошового сальдо. Протягом року треба буде поповнювати грошове сальдо 8,53 раза (А / Q* = 1 040 000 / 121 890 = 8,53).

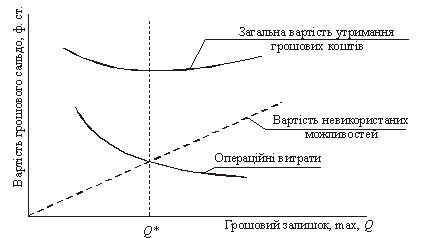
Рис. 10.3. Графічне зображення моделі Баумола[2]

Як зазначає англійський економіст Глен Арнольд, недолік моделі полягає в її несумісності з використанням овердрафту.

Модель управління грошовими
коштами Міллера—Орра

Друга модель управління грошовими коштами запропонована американськими економістами Мертоном Міллером і Даніелем Орром[3]. Модель ближча до реальності, тому що враховує невизначеність вхідних і вихідних грошових потоків. Модель Міллера—Орра зображена на рис. 10.4.

На рис. 10.4 показані коливання грошових коштів між верхньою і нижньою межами. Верхня межа, позначена буквою U*, показує максимальну суму залишку коштів, нижня L — мінімальну. Коливання залишку коштів відбувається навколо лінії С* і повертається до цієї лінії, що перебуває на відстані однієї третини від нижньої до верхньої точки. Її можна назвати точкою повернення і визначити за формулою:

.

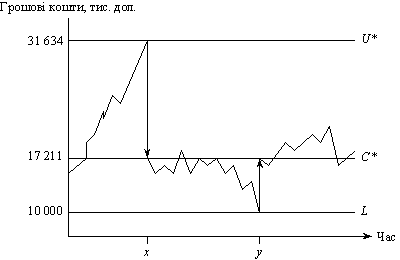
Рис. 10.4. Модель управління грошовими коштами Міллера—Орра[4]

У тому разі, коли сума грошових залишків досягає точки U* (на нижній лінії в точці х), менеджери корпорації вилучають кошти на суму U* – С* для придбання ліквідних ринкових цінних паперів, тобто поповнюють портфель цінних паперів. Грошові кошти знижуються до планового залишку. У випадку, коли сума грошових коштів опускається до нижньої межі L (на нижній лінії в точці y), корпорація продає цінні папери зі свого портфеля на суму
С* – L, грошове сальдо зростає до С*.

За моделлю Міллера—Орра використовуються ті самі умови для визначення оптимального залишку грошових коштів, що й у моделі Баумола, додається s2 — дисперсія грошових потоків.

Ситуація[5]

Припустимо, що:

1. Мінімальний залишок грошових коштів = 10 000 дол.

2. Дисперсія щоденних грошових потоків = 6 250 000 (еквівалентно стандартному відхиленню 2500 дол.).

3. Процентна ставка = 0,025 % у день.

4. Операційні витрати за кожним продажем або кожною купів­лею цінних паперів = 20 дол.

Розв’язання

1. Визначаємо суму грошового залишку між верхньою і нижньою межами:

2. Визначаємо верхню межу:

Верхня межа = Нижня межа + 21634 = 31639 дол.

3. Визначаємо точку повернення:

4. На підставі обчислених даних будуємо графік (рис. 10.4).

Практичне використання
моделі Міллера—Орра

Ситуація 1

Припустимо, що залишок коштів корпорації наближається до максимуму 31 634 дол. Що мусить зробити менеджер?

Менеджер повинен: 1) знизити залишок коштів: 31 634 –
– 17 211 = 14 423 дол.; 2) купити короткострокові ліквідні цінні папери на суму 14 423 дол., збільшивши портфель корпоративних цінних паперів.

Ситуація 2

Припустимо, що залишок коштів корпорації знизився до мінімуму 10 000 дол. Що повинен робити менеджер?

Менеджер повинен: 1) відновити кошти до суми точки повернення: 17 211 – 10 000 = 7211 дол.; 2) продати з корпораційного портфеля цінних паперів на суму 7211 дол. для поповнення залишку коштів.

Модель Міллера—Орра показує, що чим вище s2, тим більша різниця між точкою повернення і мінімальним сальдо. Чим більша невизначеність, тим вище верхня межа і чим більша варіативність, тим більша ймовірність того, що сальдо знизиться нижче мінімуму. Отже, політика, яку проводить менеджер, має бути спрямована на запобігання таким обставинам.

Таким чином, зміст обох моделей полягає у виборі між розміром операційних витрат і витрат на виплату процентів. Точка повернення за моделлю Міллера—Орра мінімізує суму операційних витрат і витрат на виплату процентів.