4.2.3. Вибір і обгрунтування форми зв'язку
Встановлення математичної форми зв'язку, тобто вибір і обгрунтування виду рівняння - найбільш відповідальний і складний етап процесу моделювання. Він полягає в знаходженні конкретного аналітичного виразу, який відображає взаємозв'язок досліджуваного показника і факторів, відібраних на попередньому етапі моделювання.
Математично задача зводиться до побудови кореляційної моделі, тобто алгебрагїчного рівняння, яке графічно може бути зображено у вигляді прямої чи то якогось типу кривої (парна кореляція ) або багатомірний простір (множинна кореляція).
Із багатьох алгебрагїчних рівнянь необхідно вибрати таку модель, яка відповідала б певним умовам:
по-перше, як це вже відмічалося, модель повинна будуватися на базі економічної теорії і відображати об'єктивні закономірності і особливості досліджуваних процесів;
по-друге, по своєму змісту модель повинна в істинному вигляді відображати структуру досліджуваного процесу; кожна змінна повинна мати певний економічний зміст;
по-третє, у модель повинні входити тільки величини, які можна вимірити;
по-четверте, система рівнянь, що формує модель, повинна задовольняти певним математичним вимогам (повнота, однорідність розмірності і т.д)
по-п'яте, бажано, щоб модель була порівняно проста для реалізації і зручною для розрахунку ряду додаткових параметрів, які мають чітко окреслений економічний зміст і інтерпретація яких значно підвищує аналітичні можливості кореляційних моделей.
Установлення форми зв'язку для економіко-статистичних моделей, в першу чергу багатофакторних, значно складніше у порівнянні з рівнянням тренда.
Це пов'язано з тим, що багатофакторні моделі характеризуються складними взаємозв'язками і взаємозалежностями окремих показників, які входять в модель.
Тому при встановленні форми зв'язку найбільш точно і достовірно її характер відображає не підібрані за певними кількісними критеріями моделі, а апробовані на реальній економічній основі моделі.
При виборі алгебрагїчної форми моделі потрібно врахувати усе, що відомо про логічні основи процесу (явища, об'єкта), використовувати накопичений
досвід раніш реалізованих моделей, які описують аналогічні досліджувані процеси.
Разом з тим не можна дотримуватися одного виду рівняння, оскільки будь-який зв'язок може бути описаний декількома видами рівнянь (останнє стосується головним чином парних моделей).
При підборі виду моделі необхідно, аналогічно рівнянням тренда, вирішити два питання: чи логічно і статистично відібрана модель адекватна реальним процесам.
Потреби логічної і статистичної адекватності моделі випливають із єдності якісного і кількісного опису досліджуваного об'єкта.
Статистична адекватність явно недостатня для практичного застосування моделі. Якщо модель демонструє явне протиріччя з економічною теорією, вона повинна виключатися з подальших досліджень.
Розбіжності між теорією і результатами математичних розрахунків свідчать про некоректність вибору рівняння. І тільки єдність якісної і кількісної сторін об'єкта (логічна і статистична адекватність) робить модель придатною для практичних розрахунків. У протилежному випадку вона не має теоретичного і практичного значення.
Нерідкі випадки, коли декілька моделей, не порушуючи логічних основ досліджуваного процесу, в різній мірі задовольняють певним статистичним характеристикам: одні задовольняють деяким критеріям краще, ніж інші, і навпаки. В таких випадках краща функція відбирається дослідником в залежності від значення певної статистичної характеристики, якій він віддає перевагу. Вибір рівняння є в більшій мірі мистецтво, ніж наука.
В принципі прогнозна модель може бути описана практично будь - яким видом алгебрагїчного рівняння .
Однак, виходячи із перерахованих раніше вимог, у економічному прогнозуванні доцільніше за все застосовувати такі види багатофокторних моделей:
лінійна
![]()
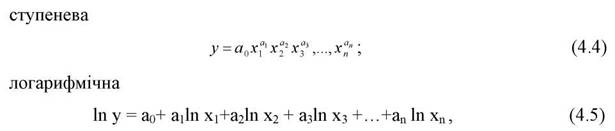
яку отримано шляхом логарифмування лівої і правої частин степеневої моделі.
Застосування логарифмічної моделі особливо доцільно при обробці динамічних рядів, оскільки логарифмування початкових даних послаблює автокореляцію у рядах динаміки і наближує розподіл до нормального (суть автокореляції буде описана у наступних параграфах).
Для перерахованих моделей легко формується система нормальних рівнянь, на основі якої визначаються параметри рівнянь а0 і аі.
Перевагою моделей (4.3-4.5) є можливість економічної інтерпретації їх параметрів (аі) і отриманих на їх основі додаткової системи показників, кожний з яких має певний економічний зміст. Параметри рівняння (аі) і система похідних показників застосовуються не тільки у аналізі, але і у прогнозуванні.
Застосування складних моделей дозволяє інколи покращити статистичні характеристики, але, як показує досвід, для практичного використання їх потрібні нерідко значні корективи, внаслідок чого втрачаються їх переваги перед більш "простими " моделями. До того ж у складних моделях параметри рівняння не мають чітко вираженої економічної інтерпретації.
Складна модель у такому випадку втрачає своє практичне значення.
На відміну від багатофакторних моделей, спектр вибору парних моделей значно ширший. У додатку 1 подані парні моделі, які широко застосовуються у економічному аналізі і прогнозуванні.
Основні принципи вибору рівняннь єдині, безвідносно чи є модель багатофакторною чи парною, хоча для останніх є деякі особливості. По-перше, значно простіше визначити природу взаємозв'язків двох економічних
Вибір необхідного рівняння із сукупності парних моделей слід, аналогічно вибору рівняння тренда, проводити у два етапи. На першому етапі, базуючись на знанні природи взаємозв'язку досліджуваних явищ, визначається лише клас рівняння. Вибір кращого рівняння, з точки зору дослідника, здійснюється шляхом порівнення ряду статистичних характеристик.
