4.2.5. Оцінка статистичної надійності моделі

Реалізована економіко-статистична модель повинна пройти ретельну перевірку на статистичну надійність. Перевірці підлягають початкові дані, параметри і характеристики моделі і власне сама модель.

Ступінь надійності параметрів і статистичних характеристик моделі є важливою умовою можливості використання її у аналізі і особливо у прогнозуванні. Необхідність статистичної оцінки рівнянь і параметрів грунтується на тому, що дослідник у практичній роботі використовує вибіркову сукупність, у той час як висновки за результатами аналізу необхідно поширити на генеральну сукупність.

Оскільки зі зміною обсягу вибіркової сукупності значення параметрів і статистичних характеристик моделей, як правило, коливаються, необхідно з певною ймовірністю бути впевненим, що значення цих показників, по-перше, не будуть рівними нулю у генеральній сукупності (спростування, так званої, "нульової гіпотези") і по-друге, величина їх буде знаходитися в певних інтервалах довіри. Оцінка надійності параметрів і статистичних характеристик моделі, відома під назвою перевірка істотності, визначається за допомогою t-критерія Стьюдента . У загальному t-критерій розраховується як співвідношення значення певного показника і його стандартної помилки.

Так наприклад, t-критерій для коефіцієнта множинної кореляції дорівнює

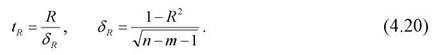
При заданому рівні істотності (Л) можна з імовірністю Р=1-А стверджувати, що коефіцієнт множинної кореляції у генеральній сукупності буде знаходитися у інтервалі

Істотність коефіцієнта регресії по t-критерію розраховується за формулою

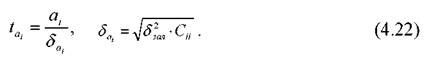
де Сіі - і-тий діагональний елемент матриці, яка зворотна до матриці системи нормальних рівнянь.

Інтервал довіри для коефіцієнта регресії розраховується аналогічно коефіцієнту множинної кореляції (умова 4.21)

Істотність рівняння перевіряється за F-критерієм Фішера

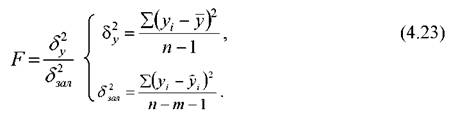
Про істотність показників і моделей можна стверджувати в тому випадку, якщо виконується умова:

де р,т - індекси слів відповідно "розрахункове" і "табличне" Складною проблемою при обробці динамічних рядів є автокореляція. Автокореляція - це зв'язок між послідовними елементами динамічного ряду, тобто зв'язок між рядами

Автокореляція не перешкоджає знаходженню зв'язку між досліджуваним показником і факторами, як і визначенню параметрів і статистичних характеристик рівняння , але вона не гарантує надійності рівняння і параметрів та можливості побудови інтервалів довіри. Отже, автокореляція більш "небезпечна" при побудові прогнозу, ніж при проведенні економічного аналізу.

Наявність автокореляції для будь-якого ряду, як правило, перевіряється за допомогою відношення фон Неймана-Харта

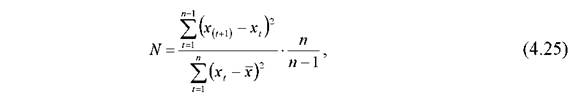
або емпіричного коефіцієнта автокореляції

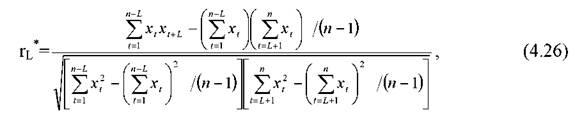
де n- число елементів вибірки;

L- лаг (як правило L=1);

t- індекс року.

Значення відношення (критерія) фон Неймана-Харта, що розраховане за формулою (4.25) порівнюється з табличними оцінками, які приводяться для

двох випадків: додатного \N"J і від'ємного N^ зв'язків.

Якщо N < N", та існує позитивна автокореляція; якщо N >NTO то залежність між відхиленнями від'ємна.

Автокореляція   ввжається   не   суттєвою,   якщо   виконується   умова

Nn <N<NO

Якщо розрахований у відповідності з формулою (4.26) емпіричний коефіцієнт автокореляції менше табличного значення, та автокореляція рядів динаміки відсутня; в протилежному випадку вона є. В дослідженнях не стільки небезпечна автокореляція початкових (мається на увазі не перетворених) рівнів ряду динаміки, скільки автокореляція залишків, тобто різниця між фактичними і розрахунковими значеннями функції.

Наявність автокореляції залишків вказує на те, що є певні закономірності зміни останніх, які можуть бути спричинені по-перше відсутністю  в моделі

важливого фактору або декількох факторів, що в значній мірі визначають зміни результативного показника, по-друге неправильним вибором форми зв'язку.

Автокореляція залишків оцінюється за допомогою d-статистики (критерії Дарбіна-Ватсона)

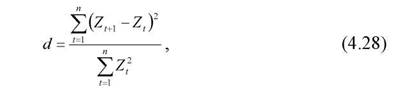
або  циклічного  коефіцієнта автокореляції залишків,  формула якого приблизно має такий вигляд:

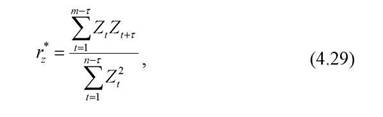
де Г-лаг (Г =l,2,3,...,L)

Для оцінки автокореляції залишків по критерію Дарбіна - Ватсона розрахункове значення dпорівнюється з табличними величинами dн і dВ, де dн -нижня, dВ - верхня границя критерія.

Якщо d<dв, то ряд має автокореляцію; якщо d>dв, то автокореляція в залишках відсутня; якщо  dH<d <dB, то необхідні додаткові дослідження

(наприклад, збільшити довжину динамічного ряду). Табличні значення критерія Дарбіна-Ватсона наводяться для позитивної (додаткової) автокореляції. Для перевірки від'ємного зв'язку рекомендується розрахувати різницю (4-d), після чого отримане значення порівнюється з dн і dв.

Істотність циклічного коефіцієнта автокореляції залишків оцінюється шляхом порівняння розрахункового значення (формула 4.28) з табличним. Якщо розрахункове значення менше табличного (по абсолютній величині), то зв'язок між залишковими відхиленнями випадковий і навпаки.

Сутність мультиколеніарності і її вплив на статистичну надійність моделі подана у п.4.2.2.