6.1.1. Прогнозування по обвідних кривих
Екстрополяція тенденцій по одному часовому ряду, яка описана в 3-й главі, базується на інерційності економічних процесів (явищ), тобто на їх властивостях зберігати в прогнозованому періоді тенденції, які склалися в "передісторії".
Методи екстрополяції по одному часовому ряду забезпечують таким чином досить високу точність прогнозу, якщо розвиток носить еволюційний характер. Однак розвиток ряду процесів, зокрема, науково- технічний прогрес, характеризується чергуванням еволюційних і революційних етапів, при яких проходять корінні зміни технологій, витрат матеріальних ресурсів, продуктивності обладнання і т.д. При наявності таких якісних стрибків зазначені методи можуть дати помилкові результати.
Це пояснюється тим, що екстрополяція тенденцій дає задовільні результати тільки на еволюційних відрізках часу. Щоб пояснити окремі тенденції, які складаються на всіх етапах розвитку процесу (еволюційного і революційного), використовується метод прогнозування по обвідних кривих.
Обвідні криві дозволяють встановити логічну послідовність, взаємозв'язок, підпорядкування тенденцій на окремих етапах в одну спільну тенденцію, яку використовують надалі для складання прогнозу.
Приклад побудови обвідної кривої подано на рис.6.1
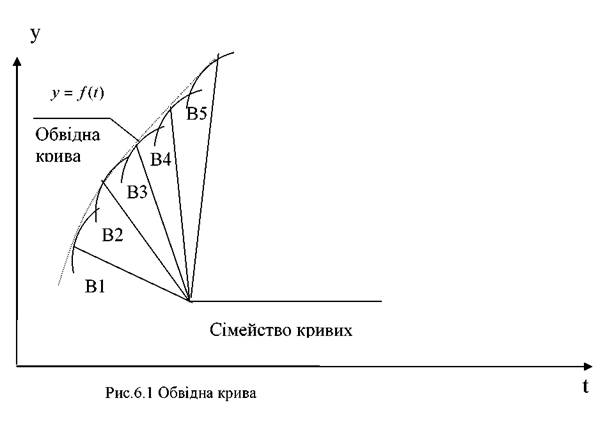
Криві Ві відображають тенденції змін процесу на окремих етапах його розвитку.
Отже, обвідна крива має дотик до всіх кривих Ві, які утворюють сукупність кривих. Для реалізації обвідної кривої в першу чергу визначається її вигляд, після чого підбирається тип кривої. Розрахунок параметрів кривої (а 0 і аі) можливо здійснити спрощеним методом. Суть цього методу полягає в наступному. За числом параметрів на графіку, побудованому за масштабом, визначається значення у по відомому значенню х. Реалізуючи одержану таким чином систему рівняннь, визначають значення а0 і аі.
Приклад. Припустимо, що обвідна крива має вигляд квадратичної функції
![]()
Оскільки рівняння (6.1) має три невідомих параметри (а0 , а1, а2), для їх обчислення необхідно побудувати систему із трьох рівнянь.
Нехай в відповідності до масштабу, прийнятому на графіку при:
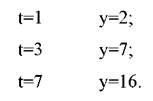
Використовуючи взаємозалежність змінних, побудуємо систему з трьох рівнянь:
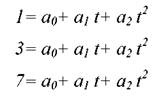
Підставивши відповідні значення t і розв'язавши систему рівнянь, одержимо значення а0 , а1 , a2. На основі рівняння 6.1, з розрахованими значеннями параметрів, можна побудувати прогноз, підставляючи послідовно значення t (t приймає значення від n+1 до n+p, де n- кількість періодів "передісторії", p- величина горизонту прогноза).
