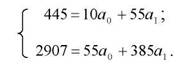3.2.1. Сутність методу екстраполяції трендів
Для аналізу тенденції на основі динамічних.рядів і побудови прогнозу з врахуванням закономірностей, що склалися в "передісторії", широко застосовується залежність , яка має назву рівняння тренда:
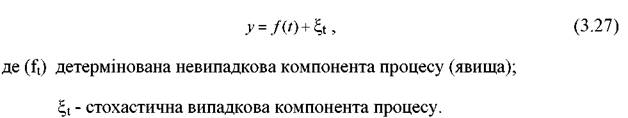
Треба мати на увазі, що в роботі розглядаються стохастичні (ймовірні) залежності.
Якщо у функціональній залежності кожному значенню аргументу (аргументів) відповідає одне єдине значення функції, то в стохастичній закономірності значенню аргументу (аргументів) відповідає не одне певне значення функції, а декілька, тобто певний розподіл цих значень. У стохастичних залежностях зв'язки не жорсткі і виявляються не в кожному окремому випадку, а лише в масі, в середньому. Це пов'язано з тим, що в стахостичних залежностях, а вони частіше мають місце у реальному житті, з ряду причин не можуть бути враховані всі аргументи (фактори). Ось чому рівняння, яке грунтується на стохастичних залежностях, складається з двох частин: детермінованої, яка формується під впливом врахованих, відомих факторів, і випадкової, яка виникає у результаті випадкових неврахованих факторів.
Тренд, який звично називають часовим трендом, відображає тенденцію зміни явища, (процесу, об'єкта) у часі.
Тренд описує фактичну усереднену для "передісторії" тенденцію процесу, що вивчається, у часі, його зовнішні прояви. Результат при цьому пов'язується виключно з плином часу. Припускається, що через фактор часу (t), можна виразити вплив усіх основних факторів, іншими словами, хоча час не являється механізмом прояву закономірностей і тенденцій, він мовби акумулює дії
основних факторів і виражає їх у рівнянні тренда. Реальний механізм впливу на значення рівней динамічного ряду у наявному виді не враховується.
Аналітичне вирівнювання тренда - це досить поширені методи прогнозування. Екстраполяція тренда може бути застосована лише у тому випадку, якщо розвиток явища достатньо добре описується побудованим рівнянням і умови, які визначають тенденцію розвитку у минулому, не зазнають значних змін у майбутньому. При до держані цих умов екстраполяція здійснюється шляхом підстановки у рівнянні тренда (3.27) значення незалежної змінної t, яка відповідає величині горизонту прогнозування.
![]()
де Р - величина горизонту прогнозування (періоди, на який складається прогноз).
У рівнянні (3.27) випадкова компонента Ј,t необхідна у подальшому для визначення уточнених характеристик прогнозу.
Рівняння тренда може бути описане широким спектром залежностей, зокрема:

Перелік рівнянь, які можуть бути використані для екстраполяції тренда, наведені в додатку 1, тільки замість фактору (X), застосовується час (t).
Для використання тренда у якості інструменту прогнозу слід чисельно оцінити параметри (коефіцієнти) рівнянь (a0,ai).
Параметри рівняння визначаються за допомогою методу найменших квадратів
де yt - фактичне значення функції;
y)t - розрахункове значення функції, яке визначається на основі відібраного рівняння.
Для лінійного рівняння залежність (3.38) може бути записана таким чином
![]()
У рівнянні (3.39) змінні yt і t являються відомими величинами, а параметри рівняння (a0,ai) - невідомими величинами. Для їх визначення слід
прирівнювати до нуля похідні від виразу (3.39) по кожному початковому параметру окремо. Після відповідних перетворень отримуємо систему нормальних рівнянь, які для лінійного рівняння тренда мають вигляд:

Для квадратичного рівняння y = a0 + a1t + a2t2 система нормальних рівнянь має такий вигляд:
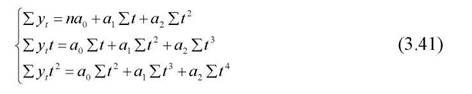
Головна проблема, яка виникає при реалізації системи нормальних рівнянь, це приведення, де це можливо, рівнянь до лінійного виду, а в деяких випадках, наприклад, для логістичної кривої і кривої Гомперца застосовують різні види перетворень, спрощення.
Якість рівняння оцінюється за системою показників (характеристик).
Найбільш суттєвим показником для оцінки кожного рівняння є коефіцієнт парної кореляції - для лінійного рівняння, і парне кореляційне відношення - для всіх нелінійних рівнянь, які відображають тісноту зв'язку між результативним показником (функцією) і факторіальною ознакою (аргументом).
Коефіцієнт парної лінійної кореляції для рівняння (yt=a0+a1t) розраховується за формулою
|
|
Парне кореляційне відношення розраховується за формулою
|
|
Про тісноту зв'язку роблять висновки з таких значень показників:
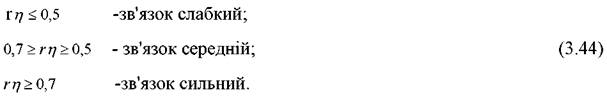
Крім тісноти зв'язку для оцінки адекватності рівняння реальним процесом служать наступні показники:
Середня помилка апроксимації

Середнє квадратичне відхилення між фактичними і розрахунковими значеннями функції:
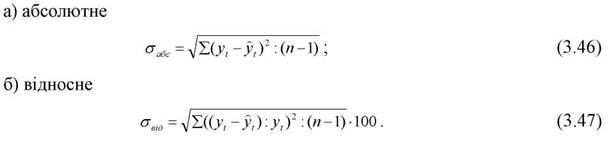
Середнє відхилення між фактичними і розрахунковими значеннями функції:
а) абсолютне

б) відносне - визначається аналогічно показнику, що розраховується за формулою (3.45)
Чим менше значення показників, які розраховані за формулами (3.45-3.48), тим вище якість відібраного рівняння. Граничний рівень встановлює дослідник, опираючись на знання, досвід, особливість даних, що аналізуються, оскільки науково обгрунтованих рекомендацій з цих питань немає.
В табл. 3.9, на прикладі даних про випуск продукції за 10 років, покажемо порядок розрахунку параметрів і статистичних характеристик для лінійного рівняння у відповідності з наведеними вище формулами.
Таблиця 3.9
Дані про динаміку випуску продукції підприємством і розрахунок
проміжних показників для визначення параметрів і статистичних
характеристик рівняння y = a0 +a1t
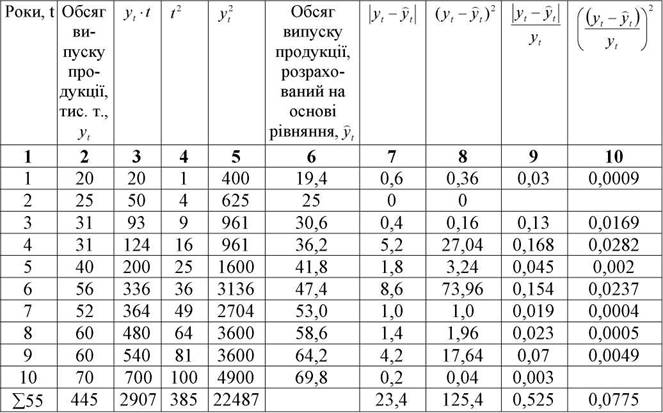
Аналогічно за таким ж принципом, тобто на основі заздалегідь розрахованих проміжних даних, визначаються параметри і статистичні характеристики інших рівнянь, зокрема квадратичного.
Підставивши отримані в таблиці 3.9 (гр. 3-10) проміжні розрахункові дані у відповідні формули, розрахуємо необхідні величини:
Параметри рівняння (a0,a1) розрахуємо на основі системи рівнянь
(формула 3.40)
|
|
Реалізувавши систему рівнянь, отримаємо:
ао=13,8; а1=5,6.
Коефіцієнт парної лінійної кореляції (формула 3.42) дорівнює:
![]()
Обсяг випуску продукції, розрахований на основі рівняння, отримаємо, якщо в рівняння підставляти послідовно за кожний рік значення аргументу (часу t).
На основі розрахованих параметрів рівняння (a0,a1) лінійне рівняння
можна записати таким чином:
![]()
Підставивши у вказане рівняння значення t за перший рік (t=1), отримаємо розрахункове значення обсягу випуску продукції за перший рік.
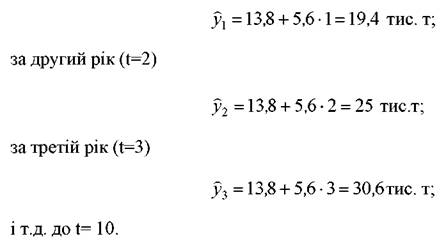
Середня помилка апроксимації (формула 3.45) дорівнює
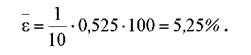
Загально прийнято, що якщо є < 10%, то побудоване рівняння характеризуєть-ся високим рівнем адекватності реальному процесу.
Середнє квадратичне відхилення між фактичними і розрахунковими значеннями функції:
а) абсолютне (формула 3.46)
![]()
б) відносне (формула 3.47)
![]()
Середнє відхилення між фактичними і розрахунковими значеннями функції:
а) абсолютне (формула 3.48)
![]()
б) відносне визначається, як відмічалося раніше, аналогічно середній
помилці апроксимації і складає відповідно 5,25%.
Запропоновані вище показники для оцінки якості рівняння не суперечать один одному.
Якими краще користуватись - це на розсуд дослідника.
В цілому ж можна констатувати, що побудоване рівняння характеризується високими і надійними характеристиками.