3.2.3. Побудова прогнозу і оцінка його якості
Інтервали довіри
Побудований на основі початкових даних "передісторії" часовий тренд, що відповідає вимогам, дозволяє використати залежність (3.49) для складання прогнозу споживання кондитерських виробів на період n+р.(Р=1,2,3,4,5)

Порівняємо фактичне споживання кондитерських виробів (t= 12-16) з прогнозними значеннями (табл. 3.12).
Таблиця 3.12 Порівняльна оцінка фактичних і прогнозних значень показника
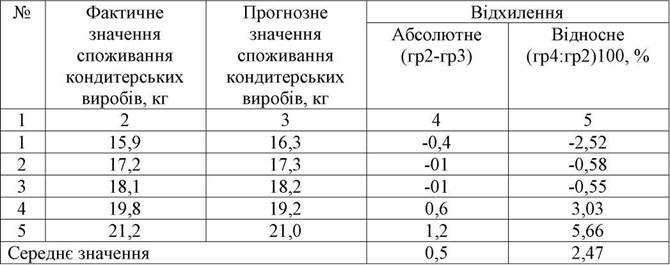
Таким чином, як засвідчують дані табл. 3.12, розроблений прогноз відрізняється достатньо високою точністю.
Щоб скласти прогноз споживання кондитерських виробів на одну людину на наступну п'ятирічку, можна поступити двояким чином: побудувати новий часовий тренд за період п=1^ 11, або використати вже наявне рівняння (3.49). Нижче подані обидва варіанти прогнозу (t=12,13,14,15,16).

Перший варіант на відміну від другого включає всю "передісторію" і тим самим більш повніше відображає тенденції споживання продукції. Разом з тим різниця невелика - в межах 0,5-0,7 кг, або 2,3-2,7 (%).
Часовий тренд (криві росту) широко застосовується для дослідження тенденції і прогнозування параметрів і функціональних характеристик машини (обладнання).
Так, на основі даних за ряд років, досліджена динаміка росту середнього значення числа символів на екрані алфавітно-цифрового дисплею. Для визначення тенденції росту названого показника були використані рівняння тренда, які містяться в табл. 3.10. Оцінка статистичних характеристик свідчить про достатньо високу адекватність рівнянь, які описують тенденції, що склалися: кореляційне відношення (коефіцієнт парної кореляції) знаходяться в межах 0,952-0,967, середня помилка апроксимації - 1,96-2,00(%).
Побудований на основі рівняння y = 2045,453 + 8,706t + 4,778t2 прогноз
показав, що на найближчідва роки, починаючи з кінця "передісторії", середнє значення числа символів на екрані алфавітно-цифрових обладнань складе відповідно 2610 і 2719 одиниць.
Область застосування рівняння часового тренда не обмежується тільки аналізом динаміки і побудови прогнозу на основі рівняння. Часовий тренд
застосовується одночасно для вдосконалення методики розрахунку ряду статистичних показників, які в свою чергу можуть бути успішно застосовані в прогнозуванні (плануванні), або іншими словами, опосередковане використання часового тренда для задач управління.
У попередньому параграфі відмічалося, що значним недоліком показників середнього абсолютного приросту і середнього коефіцієнта росту (формули 3.6 і 3.11) є залежність їх рівня тільки від крайніх значень динамічного ряду. Цей недолік в значній мірі усувається, якщо у формули підставляються не фактичні значення ряду, а вирівняні по певному рівнянню тренда. Тоді середній абсолютний приріст розраховується наступним чином
![]()
а середній коефіцієнт росту дорівнює
![]()
де f(y1);f(yn) -значення відповідно першого і останього рівнів ряду, отриманих в результаті вирівнювання ряду по відібраному рівнянню.
На відміну від фактичних даних на рівень крайніх значень вирівняного ряду впливають проміжні значення, що пояснюється процедурою реалізації системи нормальних рівнянь .
Розглянемо приклад застсуванння середнього коефіцієнту росту при формуванні асортименту продукції. В багатономенклатурних галузях формування структури асортименту є важлива і разом з тим складна задача. На практиці для цієї мети часто застосовується оцінка питомої ваги кожного виду продукції в загальній сукупності. Однак цей метод має вагомий недолік, оскільки він не враховує тенденції.
При наявності відповідного технічного і програмно-методичного забезпечення доцільно досліджувати тенденцію випуску різних видів продукції за допомогою часового тренда, а потім на основі значень середнього темпу приросту (Tnp =Kp -100-100), використавши при цьому вирівняні крайні
значення динамічного ряду, слід визначити коефіцієнт структури

При збереженні відносно стійких тенденцій випуску продукції коефіцієнт структури може бути використаний для прогнозування структури продукції у натуральному вимірі, застосувавши для цього залежність

Поняття сукупності і-того елементу не є щось постійне. Якщо, наприклад, уся продукція ділиться на декілька груп, то останні являються елементами по відношеню до всієї сукупності. В тому випадку , якщо групи діляться на окремі підгрупи, то останні являються елементами, а перші по відношенню до них сукупністю і т.д.*
За даними, які подані в табл. 3.13, розглянемо порядок використання формули (3.52) для прогнозування асортименту продукції.
* Зазначена методика формування асортимента продукції була реалізована на ЕОМ для кондитерської промисловості України.
Таблиця 3.13
Проміжні статистичні дані, які використовуються для побудови прогнозу асортименту продукції
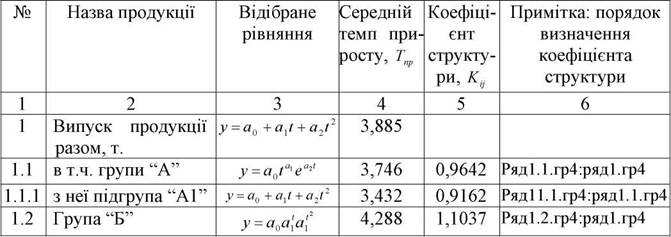
Базові значення показників: загальний випуск 570823 т.; група "А"423659т; підгрупа "А1"14250т; група "Б"147164т.
В прогнозованому періоді передбачено довести випуск усієї продукції до 574095т. Таким чином , темп приросту усієї продукції складе:
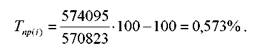
Прогнозоване значення випуску продукції у відповідності з формулою (3.53) становить:
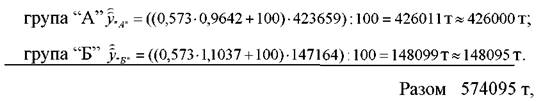
тобто загальний прогнозований обсяг групи "А" і "Б" дорівнює прогнозу загального випуску продукції.
Для визначення прогнозованого випуску підгрупи "А1" спочатку визначимо очікуваний темп приросту продукції групи "А" , оскільки вона на даному етапі стає сукупністю
![]()
Прогнозоване значення випуску продукції "А1" складає
|
|
В такому ж порядку можна визначити прогнозні значення окремих підгруп, класів і навіть видів продукції.
При відсутності технічного і програмно-методичного забезпечення для реалізації на ЕОМ рівнянь тренда можна в крайньому випадку визначити значення коефіцієнту структури на основі застосування середніх темпів приросту, розрахованих за формулою (3.11).
Заключним етапом розробки прогнозу є верифінація, яка являється процедурою оцінки достовірності, точності чи обгрунтованості прогнозу. Оцінити точність прогнозу можна тільки в двох випадках: після завершення прогнозованого періоду (здійснення події) або використання методу "прогноз екс-пост".
Показники, які використовуються для оцінки точності прогнозу, можна розділити на три групи: абсолютні, порівняльні і якісні.
До абсолютних показників відносяться :
різниця між фактичними і прогнозними значеннями
![]()
середня помилка прогнозу
![]()
де n-це горизонт прогнозу; відносна помилка прогнозу
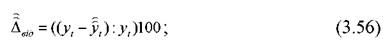
середня відносна помилка прогнозу
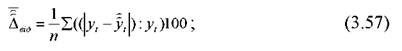
(значення перерахованих вище показників оцінки прогнозу містяться в таблиці(3.12);
середня квадратична абсолютна помилка прогнозу

Порівняльні показники точності прогнозів грунтуються на порівнянні помилки даного прогнозу з еталонним прогнозом
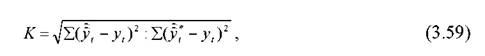
де y))t* - прогнозоване значення еталонного прогнозу. До порівняльних показників можна також віднести:
Коефіцієнт невідповідності Г. Тейла
![]()
коефіцієнт кореляції між прогнозованими та фактичними значеннями показників
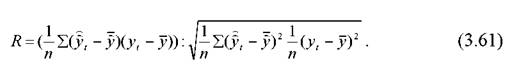
Для прогнозу, дані якого подані в табл. (3.12), перераховані вище показники оцінки точності дорівнюють:![]()
Якісні показники точності прогнозу базуються на розкладанні помилок прогнозування на певні складові. Так, пропонується розкласти середній квадрат помилки прогнозу на три частини: частку зміщення, частку дисперсії, та частку ковариації*.
Вибір показників точності прогнозу залежить від об'єкту прогнозування і тих задач, які ставить перед собою дослідник у відношенні точності прогнозу.
Наведені в табл. 3.12 прогнозні значення відображають точкову оцінку. Збіг точкового прогнозу з фактичними даними малоймовірний. Тому в прогнозуванні використовуються інтервальні значення прогнозу у вигляді "вилки"-максимальна і мінімальна величина.
Інтервали довіри прогнозу можуть бути записані наступним чином:
*Детальніше див.: Тейл Г. Экономические прогнозы и принятие решений. Пер. с англ.М.: "Статистика", 1971, с 39-40.
![]()
де Р-величина горизонту (для п'ятирічки Р відповідно набуває значення 1,2,3,4,5)
ta -значення t-критерію Стьюдента (табличне) з (n-1 ) ступенями свободи
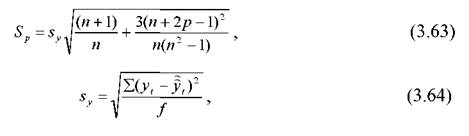
де yt і y)t -відповідно фактичне і розрахункове значення рівнів ряду ;
f-число ступенів свободи, яке визначається в залежності від числа спостережень ряду (n) і числа параметрів тренда , що оцінюються (для прямої лінії f=n-2).
На основі даних табл. 3.11 розрахуємо sy, враховуючи при цьому, що
різниця yt-yt знаходиться в гр4; період передісторії n=6
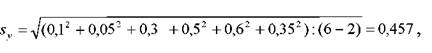
t-критерій Стьюдента з числом ступенів свободи (n-1 ) = 6-1 = 5 і рівнем істотності 0,5% дорівнює 2,57.
Розрахунки інтервального прогнозу наведені в табл. 3.14.
Таблиця 3.14 Розрахунок інтервалів довіри прогнозу для лінійного тренда
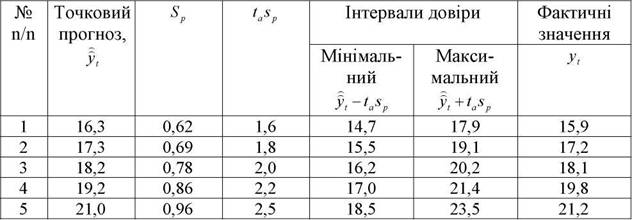
Таким чином, як засвідчують дані табл. 3.14, фактичні значення показників знаходяться в середині інтервалів довіри. Наявність мінімального і максимального значення прогнозованого показника дозволяє по суті розробити альтернативні варіанти стратегії дій підприємства з врахуванням можливих ситуацій на ринку.
