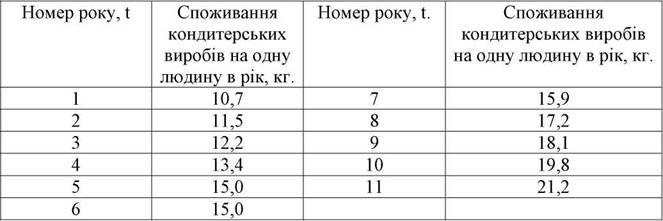
3.1.1. Екстраполяція на основі аналітичних показників рядів динаміки
Динамічним рядом (рядом динаміки) називається послідовність показників, які характеризують зміну явища (процесу, об'єкта) у часі. Окремі спостереження динамічного ряду називаються рівнями.
За часом, відображеним у динамічних рядах, вони поділяються на моментні і інтервальні.
В моментних рядах динаміки рівні виражають величину явища на відповідну дату, наприклад, залишки готової продукції на перше число кожного місяця , вартість основних фондів на початок, чи кінець року та ін.
В інтервальних рядах рівні виражають розміри явищ за проміжок часу, наприклад, випуск продукції за місяць, квартал, рік.
При побудові динамічних рядів слід в першу чергу приділити увагу на порівнянність рівнів ряду. Це значить, що усі рівні повинні виражатися в однакових одиницях виміру, розраховуватися по єдиній методології, включати єдине коло об'єктів.
Позначивши:
у1 - початкове значення рівня динамічного ряду;
уn - кінцеве значення рівня динамічного ряду;
Уі - умовно прийнятий (і-тий) рівень динамічного ряду;
п - кількість елементів динамічного ряду,
наведемо основні аналітичні показники динамічного ряду, які використовуються в прогнозуванні:
1. Абсолютний приріст:
1.1 Ланцюговий
![]()
1.2 Базисний
![]()
2. Середній абсолютний приріст

3. Коефіцієнт росту:
3.1. Ланцюговий

3.2. Базисний

3.3 Завесь період

4. Коефіцієнт приросту
![]()
5.Середній коефіцієнт росту

6. Сере дній коефіцієнт приросту
![]()
7.Абсолютний розмір 1% приросту:
7.1. Ланцюговий
•/ і—1
і—1
7.2. Завесь період

8. Коефіцієнт випередження (відставання)
![]()
Добуток ланцюгових коефіцієнтів росту дорівнює базисному коефіцієнту росту за весь період, тобто
![]()
що може бути доведено таким чином.
Нехай маємо динамічний ряд за 5 років та рівень показника за базисний рік, що передує рокам п'ятирічки (у0). Добуток ланцюгових коефіцієнтів росту складе
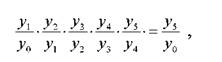
тобто підтверджується залежність (3.16)
На основі наведених аналітичних показників, які широко застосовуються для оцінки динамічних рядів, можна вивести залежності, що можуть бути використані для побудови прогнозів:
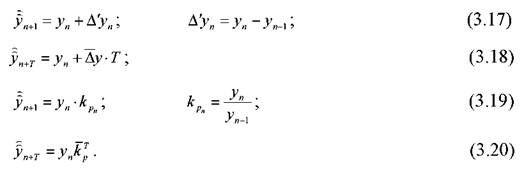
де у — тут і далі таким чином позначаються прогнозні значення показника.
Т - величина горизонту прогнозу (Т=1 ;2;3...).
Практичне застосування зазначених залежностей покажемо на прикладах.
Приклад 1.
В таб. 3.1 наведені дані про середнє споживання кондитерських виробів на одну людину по області за рік. Використовуючи залежності (3,18 та 3,20), побудуємо прогноз споживання кондитерських виробів на наступну п'ятирічку.
|
|
| Таблиця 3.1 |
| Середньорічне споживання кондитерських виробів по області |
В табл. 3.1 наведені данні по двох п'ятирічках та базисному року.
Остаточно про якість прогнозу можна судити лише після того, як подія відбулася. Щоб оцінити надійність застосованого методу, використовуються, так званий, метод «прогноз екс-пост». Суть його полягає в наступному.
Початкові дані діляться на дві частини (два періоди) : 1 -г- к і (к+1)^-п. За даними першої частини, умовно прийнятої за "передісторію", будується рівняння (модель), на базі якої складається прогноз для другої частини (другого періоду), результати якого потім порівнюються з фактичними даними. Такий підхід застосовується і для інших кількісних методів прогнозування.
Використовуючи дані перших шести років - базисний рік та роки першої п'ятирічки, розрахуємо відповідно:
Середній абсолютний приріст
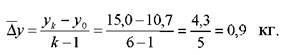
Середньорічний коефіцієнт росту
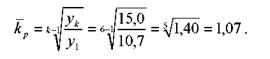
На основі залежності (3.18) складемо прогноз споживання кондитерських виробів на період (к+1) ^ n
![]()
41
![]()
Результати розрахунків зведені в таблицю та порівняні з фактичними даними.
Таблиця 3.2
Оцінка якості прогнозу, складеного на основі середнього абсолютного
приросту
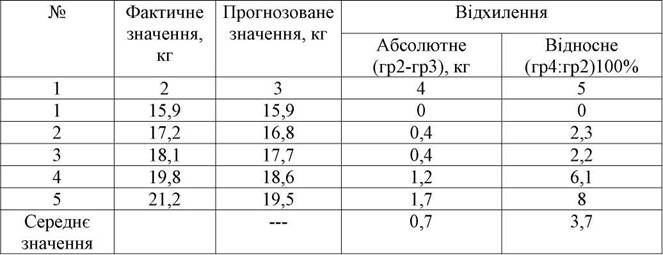
Складемо прогноз споживання кондитерських виробів на основі залежності (3.20)
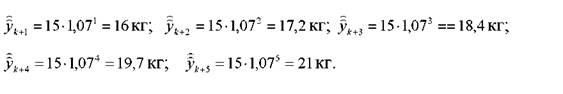
Результати прогнозу порівняні із фактичними даними та оцінена якість прогнозу (табл.3.3).
Таблиця 3.3
Оцінка якості прогнозу, складеного на основі середньорічного
коефіцієнта росту.
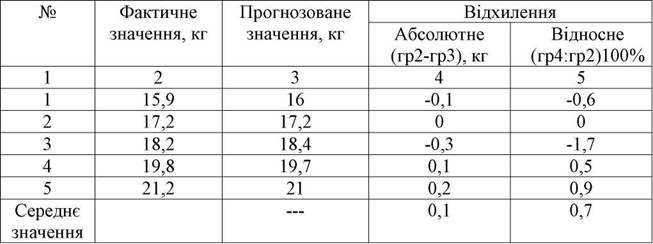
Порівнюючи результати прогнозів, поданих в табл.3.2 та табл. 3.3, можна зробити висновок про те, що використання середньорічного коефіцієнта росту забезпечує більш високу точність прогнозу, про що свідчать відхилення за всі роки і в цілому за п'ятиріччя.
Для складання прогнозу за межі наявних даних, тобто на перспективу, розрахуємо середньорічний коефіцієнт росту на основі другої п'ятирічки з використанням базисного періоду.
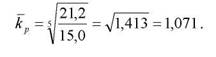
Прогноз споживання кондитерських виробів на наступне п'ятиріччя складе:![]()
![]()
Прогноз споживання кондитерських виробів складено з врахуванням зберігання тенденцій, які склалися в "передісторії".
Суттєвим недоліком показників середнього абсолютного приросту та середнього коефіцієнта росту є те, що значення їх цілком залежить тільки від крайніх рівнів динамічного ряду. Проміжні значення, які багато в чому, а іноді і в вирішальній мірі визначають тенденцію змін показників, по суті в розрахунках не беруть участі. Зазначений недолік багато в чому усувається
шляхом аналітичного вирівнювання рядів динаміки, що буде розглянуто у наступному параграфі.
Приклад 2
В управлінні бурякоцукровим виробництвом дуже важлива об'єктивна оцінка очікуваних урожайності та цукристості буряка, на основі яких визначається валовий збір буряка та обсяг виготовленого цукру. Першочергове значення мають короткострокові прогнози показників, що орієнтовані на поточний виробничий рік, який охоплює приблизно період вересень-січень.
В основу розрахунків середньої урожайності буряка та середньої цукристості заготовленого буряка покладені значення вказаних показників за станом на перше жовтня.
Для одержання названих показників у агропромисловому комплексі щодекадно робляться оцінки маси кореня (з 1 липня по 1 жовтня) та цукристості буряка (з 20 липня по 1 жовтня). Задача полягає у тому, щоб на основі одержаних даних, оцінити значення цих показників за станом на 1 жовтня.
З множини методів, які рекомендовані для оцінки значення зазначених показників на 1 жовтня, найбільш простий та доступний - це використання значень приросту буряка між суміжними декадами. Для розрахунку приросту використовуються середні значення маси кореня на кожну декаду, яка визначається за формулою:

![]()
В табл. 3.4 наведені дані про абсолютні прирости маси кореня, які розраховані на основі середніх значень маси кореня за 10 років.
Таблиця 3.4
Абсолютні прирости маси кореня (г) по Вінницькому облбурякоцукропрому
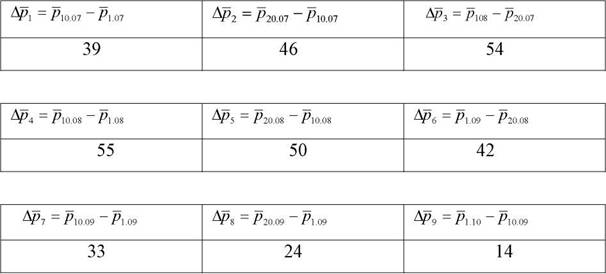
Отримавши данні про масу кореня за станом на 1.07, можна, використовуючи показники табл. 3.4, визначити очікуване значення названого показника за станом на 1.10
![]()
Якщо поступає інформація за наступні декади, то розрахунки виконуються таким чином:
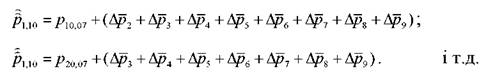
Припустимо, за станом на 1.07 поточного року маса кореня становила 25г. Тоді очікувана маса кореня за станом на 1.10 становить
![]()
В табл. 3.5 наведені результати послідовних прогнозів на основі застосування абсолютних приростів.
| Таблиця 3.5 |
| Результати прогнозу маси кореня по Вінницькому облбурякоцукропрому |
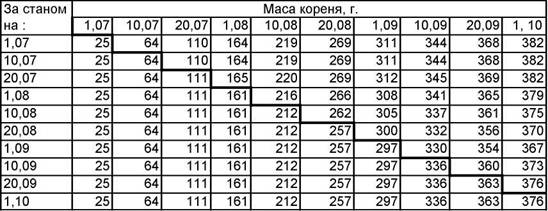
Примітка: Над рискою табл. 3.5 подані прогнозовані значення, під рискою - фактичні.
Результати прогнозу достатньо точні. Враховуючи, що фактичне значення маси кореня за станом на 1.10 дорівнює 376г, то розходження по той, чи інший бік становило від 376-382=-6г, або 1,6%, до 376-367=9г, або 2,4%.
За таким ж самим методом прогнозується цукристість буряка.
Слід відмітити, що прогнозування найважливіших показників буряко-цукрового виробництва було реалізовано на ЕОМ і функціонувало у реальному режимі часу для Вінницького облбурякоцукропрому і Укрбурякоцукропрому протягом тривалого часу.