2.2.3.1.6. Кореляційно-регресійний аналіз
Якщо ДА дає змогу констатувати факт наявності зв'язків досліджуваної випадкової величини з одним або кількома незалежними факторами, то за допомогою кореляційно-регресійного аналізу (КРА) виявляють "ступінь щільності" цих зв'язків, їхню спрямованість і форму (кількісні оцінки параметрів моделей, що описують відповідні процеси). У практиці СР можливі ситуації, коли захід,
що поліпшує якусь одну сторону життєдіяльності людини, одночасно негативно позначається на інших її сторонах. Наприклад, створення кращих умов для занять молоді спортом може спричинити зниження інтересу до навчання. Це відбувається через незнання кореляції різних факторів з досліджуваною величиною* та між собою. Кореляційно-регресійний аналіз допоможе менеджерові СР розібратися в хитросплетінні можливих причин виникнення будь-якої соціальної ситуації і прийняти правильне рішення.
Статистичні зв'язки описуються в КРА шляхом побудови так званої функції регресії (ФР), що найкращим чином, у смислі деякого критерію, наближає (апроксимує) значення залежної змінної. За такий критерій найчастіше вибирають мінімум суми квадратів відхилень (неув'язок) результатів спостережень залежної змінної (реалізацій) від значень, отриманих розрахунком за рівнянням регресії (РР) для тих самих значень фактора (факторів)**. При цьому вигляд ФР (структура моделі процесу) задається апріорі, на підставі уявлень про природу процесів, що пов'язують залежну та незалежні змінні, або підбирається у процесі обчислень (покрокова та гребенева регресії). В усіх варіантах мінімум суми квадратів неув'язок (звідси назва — метод найменших квадратів, або МНК) досягається шляхом підбору параметрів (коефіцієнтів) PP. Лінійну залежність двох змінних (лінійна однофакторна модель, або ЛОМ) зображають у вигляді:
![]()
де Y. та X. — реалізації залежної та незалежної змінної у /-му спостереженні; Е. — похибка наближення (неув'язка, залишок).
Розв'язання задачі МНК було розпочато у працях Лежанра (1805), Гаусса (1809) та Маркова (1904). Відтоді теорія МНК суттєво розвинулася, а завдяки комп'ютерним технологіям стало можливим виявляти та описувати статистичні зв'язки за допомогою широкої гами моделей (лінійних та нелінійних). Кількість коефіцієнтів у лінійних багатофакторних моделях (ЛБМ)
![]()
та в нелінійних багатофакторних моделях (НБМ)
![]() Далі залежно від контексту будуть використовуватися синоніми: ознака, варіанта, відгук, результативна величина, залежна змінна.
Далі залежно від контексту будуть використовуватися синоніми: ознака, варіанта, відгук, результативна величина, залежна змінна.
В КРА використовуються також синоніми цього терміна: незалежна змінна, предиктор, регресор.
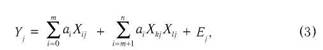
де k = 0; / = 0; k Ф /, може сягати сотень і навіть тисяч найменувань і розв'язання таких громіздких систем рівнянь без високопродуктивних ЕОМ і ефективних алгоритмів неможливе. Не всі коефіцієнти регре-сійних моделей мають смислове наповнення, тобто модель є формальною, але рівняння моделі можна використовувати для статистичного прогнозування (екстраполяції) — оцінювання очікуваного значення залежної змінної для значень предикторів, що перебувають поза інтервалом їх спостереження. Коефіцієнти, що стоять при перших степенях регресорів в описаних моделях, виражаються через вибіркові коефіцієнти лінійних парних кореляцій між регресорами (позначаються г, або р), а саме рівняння регресії з їх допомогою може бути записане через кореляційну матрицю гхх (позначається R) і вектор коефіцієнтів парної кореляції між регресорами та залежною змінною
![]()
де: (З — вектор бета-коефіцієнтів регресійної моделі.
Коефіцієнт регресії є безрозмірною величиною, що змінюється в межах від -1 до +1. Рівність г = 0 означає відсутність лінійної залежності, але не виключає нелінійної. Чим ближче | г | до одиниці, тим "тісніший" лінійний зв'язок між двома випадковими величинами і тим менше СКВ подання кожної з них через лінійну функцію від іншої. Знак г визначає напрямок зв'язку (плюс — прямий, мінус — зворотний). Для ЛММ обчислюється також коефіцієнт множинної (сукупної) кореляції, який ще називається коефіцієнтом детермінації (позначається R2). Він показує, наскільки варіація результативної величини зумовлена варіаціями всіх факторів. Знаючи г та г , можна розрахувати часткові коефіцієнти кореляції rYX(x } між результуючою величиною і кожним з факторів при елімінуванні (виключенні) впливу всіх інших факторів. Інакше кажучи, часткові коефіцієнти кореляції відображають ступінь "чистого" впливу факторної ознаки на результуючу.
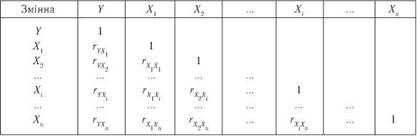
Алгоритм КРА має такий вигляд. На першому етапі за даними первісних спостережень (табл. 1) обчислюється симетрична матриця коефіцієнтів парної кореляції, або кореляційна матриця (КМ) (табл. 2).
|
|
|
|
| Таблиця 1 |
| Таблиця 2 |
Далі аналізується перший стовпчик (вектор) КМ на предмет виявлення незначущих зв'язків з використанням ґ-критерію. Виявлені у такий спосіб другорядні фактори видаляються (викреслюванням відповідних рядків і стовпчиків). Після цього стовпчики перетвореної KM, починаючи з другого, аналізуються на мультиколінеарність, тобто на залежність факторів один від одного. Справа в тому, що кореляція факторів збільшує похибки коефіцієнтів регресії, що робить рівняння регресії непридатним для аналізу та прогнозування. За критерій мультиколінеарності беруть виконання таких нерівностей при доборі факторів для подальшого аналізу:
![]()
Якщо ці нерівності (або хоч одна з них) не виконуються, то відкидається той фактор, зв'язок якого з результуючою ознакою найменш щільний.
На другому етапі КРА обчислюється величина R2. Чим ближча вона до 1, тим менша роль неврахованих у моделі факторів і тим
більше підстав для висновку, що модель повна й адекватно описує досліджуване явище.
На третьому етапі КРА будується власне функція регресії. Для лінійної моделі застосовується МНК [20]. Коефіцієнти нелінійних регресійних моделей розраховуються за допомогою ітераційного МНК або оптимізаційних методів [18]. Обчислювання коефіцієнтів регресії супроводжується оцінюванням їхньої значущості (статистично незначущі коефіцієнти відкидаються, модель уточнюється) та дисперсійним аналізом: оцінкою дисперсії результативної ознаки (повна дисперсія) та оцінкою дисперсії результатів спостережень (залишкова дисперсія). Різниця між цими величинами є часткою повної дисперсії, що пояснюється існуванням регресійних зв'язків між залежною і незалежними змінними. Крім того, обчислюється довірчий інтервал для відхилень розрахованої (емпіричної) кривої від дійсної (теоретичної) кривої регресії, що дає змогу побудувати так званий коридор помилок.
На четвертому етапі КРА створюється матриця часткових коефіцієнтів кореляції, за якою можна оцінити ступінь елімінованого впливу факторів на результативну змінну. Як правило, часткові коефіцієнти кореляції виявляються меншими за парні. Це пояснюється тим, що з них виключено непряму частку впливу факторів на результативну змінну, яка зумовлена кореляцією факторів між собою.
Якщо КРА виконано правильно, "залишки" Е. розподіляються за нормальним ЗРЙ, а коефіцієнти рівняння регресії служать кількісними оцінками впливу відповідного фактора на результативну ознаку при незмінності інших. Коефіцієнт детермінації свідчить про повноту впливів.
|
|
| де Sx та SY — стандартні помилки відповідно незалежної та залежної змінних. |
| 216 |
Коефіцієнти регресії мають різні розмірності (одиниці вимірювання), через що їх неможливо порівнювати, якщо виникло питання про порівняльну "силу" впливів факторів на результат. Щоб надати коефіцієнтам регресії порівняльного вигляду, їх виражають у частках СКВ (так звані стандартизовані, або (З-коефіцієнти):
Крім того, для оцінки відносної зміни результативної змінної через зміну фактора використовують так званий коефіцієнт еластичності (КЕ)
![]()
де риска означає усереднення за кількістью спостережень. Коефіцієнт еластичності показує, на скільки відсотків у середньому змінюється результативна змінна при зміні фактора на 1 %.
Слід зазначити, що на практиці використовують й інші характеристики ступеня щільності статистичних зв'язків. Для малих вибірок застосовують коефіцієнт Фехнера. Для аналізу зв'язків між атрибутивними ознаками використовують коефіцієнти кореляції рангів Спірмена і тау-б Кендалла, асоціації Д. Юла, контингенції Пірсона. Коли тип розподілу досліджуваної ознаки невідомий, застосовують критерій серій та критерій інверсій (непараметричне оцінювання) [3] та ін.
В MS Excel KPA представлений інструментами Пакета анализа данных: Корреляция, Ковариация та Регрессия, а також процедурами побудови ліній тренду. За допомогою перших двох інструментів розраховують відповідно кореляційну (табл. 2) та коваріацій-ну матриці, елементи яких пов'язані відношенням
![]()
де cov(X.,Y.) — елемент коваріаційної матриці; SX,SY — стандартні похибки відповідно незалежної та залежної змінних.
Розрахунки кореляції та коваріації для окремої пари даних виконують за допомогою статистичних функцій КОРРЕЛ і КОВАР.
Інструмент MS Excel Регрессия орієнтований на побудову лінійних одно- та багатофакторних моделей за процедурою МНК. Програма виводить коефіцієнти регресії та їхні стандартні помилки; масив значень, розрахований за рівнянням регресії; коефіцієнт детермінованості; стандартну похибку оцінки результативної змінної; регресійну і залишкову суму квадратів та інші характеристики. Крім того, залишки можна включити у вихідний блок, побудувати діаграми залишків для кожного фактора та накласти на них графіки нормального ЗРЙ.
Для побудови ЛМ-моделей в MS Excel використовують функцію ЛИНЕЙН. Вона задіяна в процедурі Пакет анализа, але, як і
інші функції, може використовуватися користувачем незалежно (без виклику Пакет анализа) та з іншими функціями як вкладена. Наприклад, для ЛОМ комбінація ИНДЕКС (ЛИНЕЙН(...)) дає змогу отримати тангенс кута нахилу графіка прямої регресії до осі значень незалежної змінної (вісь ОХ) та величину відрізка, що відсікається цією прямою на осі значень залежної змінної (вісь OY). Такі ж величини повертають функції НАКЛОН і ОТРЕЗОК. Функція СТОШУХ повертає стандартну помилку прогнозованого значення залежної змінної для кожного значення незалежної змінної.
Під трендовим аналізом в MS Excel розуміють МНК-апроксимацію однофакторних залежностей з використанням різних моделей: прямої лінії (У = а0 + ахХ), поліноміальної (У = aQ + ахХ + + а2Х2 + ... + + а6Х6), логарифмічної (У = а + b \пХ), експоненціальної (У = аеьх) та степеневої (У = аХь). Лініями тренду (ЛТ) можна доповнювати ряди даних, які подані на ненормованих плоских діаграмах з областями, лінійчастих, біржових, точкових та пузиркових діаграмах, гістограмах і графіках. Лінії тренду можна також використовувати незалежно від діаграм (команди ВСТАВКА/ЛИНИЯ ТРЕНДА).
В системі STATISTICA КРА представлений значно ширше. Трен-довий аналіз збагачено сплайн-апроксимацією та можливістю застосовувати функцію, задану користувачем. До регресії можна одночасно включати кількісні та описові змінні (що набувають, наприклад, значення 0 або 1). Коефіцієнти ЛБМ подано в стандартизованому вигляді ((З-коефіцієнтів). У модулі Multiple Regression (Множинна регресія) передбачено спеціальне діалогове вікно, в якому виконується всебічний аналіз залишків (ResidualAnalysis). Зокрема, розраховується регресія залишків, будується коридор помилок і візуально перевіряється, чи є відхилення від нормального ЗРЙ залишків. Якщо підозра підтверджується, до первісних даних можна застосувати лінійні перетворення: логарифмування або добування квадратного кореня, а за допомогою інструмента Brushing (Пензель) в інтерактивному режимі проаналізувати будь-які точки на графіку регресії. Крім того, в STATISTICA є кілька програм, написаних мовою STATISTICA BASIC, які реалізують такі методи: зважений (узагальнений) МНК (модуль wes.stb), двокроковий МНК (модуль 2stls.stb) та оцінювання параметрів моделей з дуже великою кількістю предикторів (модуль regression, stb).